• Notas
• 6to Semestre
• Control

Análisis de la respuesta en el tiempo de sistemas lineales

Se puede analizar para los dos estados de un sistema lineal:

• Estado transitorio
• Estado estacionario

Estado transitorio

Sistemas de primer orden

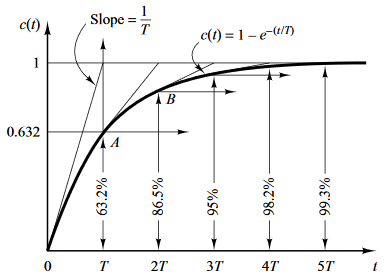
El parámetro importante es la constante de tiempo $T$. Pues la respuesta llega al 98% de su valor final en $4T$. Se considera que ahí termina el transitorio y comienza el estado estacionario.

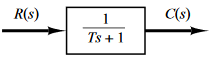
Sistemas de segundo orden

Tienen la siguiente función de transferencia general:

\[\dfrac{C(s)}{R(s)}=\dfrac{\omega_n^2}{s^2+2\xi\omega_n s +\omega_n^2}\]

Análisis de la respuesta al impulso

• Los polos del sistema son:

\[s_{1,2}=-\xi\omega_n\pm\omega_n\sqrt{\xi^2-1}\]

\[\cos\beta=\xi\\\beta=\arccos{\xi}\]

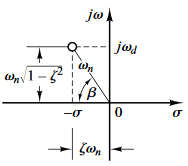
• La forma de la respuesta depende de $\xi$

Caso	Amortiguamiento	Polos	Respuesta
$\xi=0$	No hay amortiguamiento	Imaginarios e iguales	Senoidal
$0\lt\xi\lt1$	Subamortiguado	Imaginarios y diferentes	Oscila y se atenúa
$\xi=1$	Criticamente amortiguado	Reales e iguales	Exponencial
$\xi\geq1$	Sobreamortiguado	Reales y diferentes	Exponencial

Análisis de la respuesta al escalón unitario

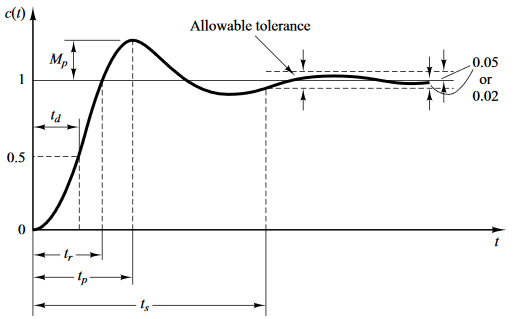
Nos centramos en el caso donde $0\lt\xi\lt1$:
Se definen:

• El tiempo pico $t_p$

\[tp=\dfrac{\pi}{\omega_n\sqrt{1-\xi^2}}\]

• El máximo sobre impulso $M_p$

\[M_p=\dfrac{c(t_p)-c(\infty)}{c(\infty)}100\%\quad\quad M_p=e^{-\frac{\pi\xi}{\sqrt{1-\xi^2}}}\ 100\%\]

• El tiempo de establecimiento $t_s$

\[t_s=\dfrac{4}{\xi\omega_n}\]

Estado estacionario

Teorema del valor final

Establece que el límite cuando el tiempo tiende a infinito de una función que depende del tiempo, es igual al producto de la variable $s$; en el dominio de Laplace, por la transformada de Laplace de dicha función.

\[\lim_{t \rightarrow \infty} f(t) = \lim_{s \rightarrow 0} s\mathcal{L}\left\{f\right\}(s)\]

Por lo que:

\[\lim_{t \rightarrow \infty} y(t) = \lim_{s \rightarrow 0} sY(s)\]

Error en el estado estacionario

\[E(s)=\dfrac{1}{1+G(s)}R(s)\] \[e_{ss}=\lim_{t\rightarrow\infty}e(t)\stackrel{\text{t. valor final}}{=}\lim_{t\rightarrow\infty}sE(t)=\lim_{s\rightarrow 0}{\dfrac{sR(s)}{1+G(s)}}\]

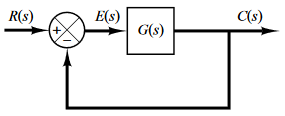
El error $E(s)$ depende de:

• Entrada $R(s)$
• TIPO del sistema $G(s)$:

  TIPO del sistema

  El tipo de sistema es la cantidad de polos de G(s) en el origen del plano de Laplace.

Considerando la función de transferencia G(s) general:

\[G(s)H(s)=\dfrac{K(T_a s + 1)(T_b s + 1)\ldots(T_m s + 1)}{s^N(T_1 s + 1)(T_2 s + 1)\ldots(T_p s + 1)}\]

Donde:
$K$ = Ganancia en lazo abierto.
$s^N$ = Polo de multiplicidad $N$ en el origen.

El TIPO del sistema sería la multiplicidad del polo en el origen $N$

El TIPO de sistema está relacionado con la precisión, mientras más grande sea el tipo de sistema, mayor será la precisión pero peor, será la estabilidad.

Constante del error de posición (escalón) $K_p$

Cuando la entrada es un escalón unitario.

\[c(t)=\begin{cases} 0 & t<0\\ 1 & t>0\\ \end{cases}\]

Dado que la transformada de Laplace está definida para $t>0$:

\[C(s)=\dfrac{1}{s}\]

Aplicando la expresión del error:

\[\begin{aligned} e_{ss}&= \lim_{s \rightarrow 0} \dfrac{s\dfrac{1}{s}}{1 + G(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{1 + G(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{1 + Kp}\\ \end{aligned}\]

Por lo que, $Kp$ queda definida de la siguiente forma:

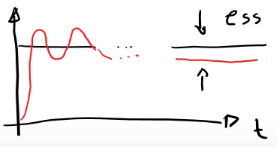
\[Kp=\lim_{s \rightarrow 0} G(s)\]

Esta constante describe la capacidad de un sistema con retroalimentación para reducir o eliminar el error de posición en el estado estable.

Constante del error de velocidad (rampa) $K_v$

Cuando la entrada es una rampa unitaria.

\[c(t)=|t|\]

Dado que la transformada de Laplace está definida para $t>0$:

\[C(s)=\dfrac{1}{s^2}\]

Aplicando la expresión del error:

\[\begin{aligned} e_{ss}&= \lim_{s \rightarrow 0} \dfrac{s\dfrac{1}{s^2}}{1 + G(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s[1 + G(s)]}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s + sG(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s + Kv}\\ &= \dfrac{1}{Kv}\\ \end{aligned}\]

Por lo que, $Kv$ queda definida de la siguiente forma:

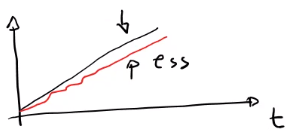
\[Kv=\lim_{s \rightarrow 0} sG(s)\]

Esta constante describe la capacidad de un sistema con retroalimentación para reducir o eliminar el error de velocidad en el estado estable.

Constante del error de aceleración (parábola) $K_a$

Cuando la entrada es una parábola.

\[c(t)=\dfrac{1}{2}t^2\]

Se obtiene su transformada de Laplace.

\[C(s)=\dfrac{1}{s^3}\]

Aplicando la expresión del error:

\[\begin{aligned} e_{\infty}&= \lim_{s \rightarrow 0} \dfrac{s\dfrac{1}{s^3}}{1 + G(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s^2[1 + G(s)]}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s^2 + s^2G(s)}\\ &= \lim_{s \rightarrow 0} \dfrac{1}{s^2 + Ka}\\ &= \dfrac{1}{Ka}\\ \end{aligned}\]

Por lo que, $Ka$ queda definida de la siguiente forma:

\[Ka=\lim_{s \rightarrow 0} s^2G(s)\]

Esta constante describe la capacidad de un sistema con retroalimentación para reducir o eliminar el error de aceleración en el estado estable.

Relación del TIPO de sistema y los errores

Esto se puede ver, analizando el error para los diferentes tipos de sistema:

	Error de posición	Error de velocidad	Error de aceleración
Sistema TIPO 0	$\dfrac{1}{1+K}$	$\infty$	$\infty$
Sistema TIPO 1	0	$\dfrac{1}{K}$	$\infty$
Sistema TIPO 2	0	0	$\dfrac{1}{K}$

Por lo general sólo se analiza hasta sistemas de tipo 3, porque la estabilidad suele ser muy mala para sistemas de tipo mayor.

Incremento del TIPO de sistema

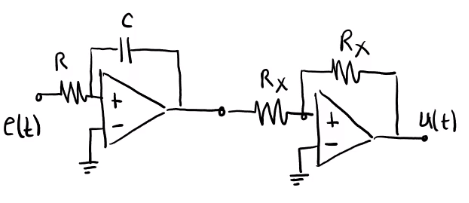
Para incrementar el tipo de sistema se debe utilizar un integrador:

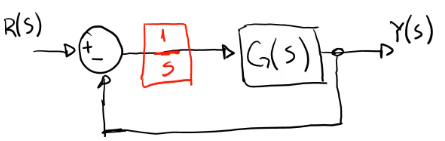
Por ejemplo, tratandose de sistemas electrónicos analógicos, se pueden utilizar dos aplificadores operacionales, uno en configuración integrador inversor y otro en inversor:

\[\dfrac{U(s)}{E(s)}=\left(-\dfrac{1}{RCs}\right)\left(-\dfrac{R_x}{R _x}\right)=\dfrac{ \frac{1}{RC} }{s}\]