Circuitos magnéticos
La dirección de la corriente se conoce usando la convención de la mano derecha.
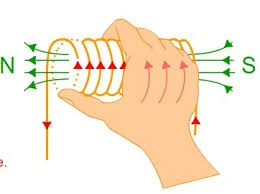
Se utilizan núcleos magnéticos para concentrar el flujo magnético en formas deseadas y poder redirigirlo.
Propiedades magnéticas del núcleo
Las propiedades magnéticas del material se definen en función de la magnetización $M [\frac{A}{m}]$ y la intensidad de campo magnético $H [\frac{A\ vuelta}{m}]$. Las unidades son así porque la magnetización depende intrínsecamente solo del material, mientras que la intensidad de campo también depende de la confuguración.
Circuitos magnéticos
Para aplicaciones magnéticas, en donde se requiere generar fuerzas de carácter megnéticas, es conveniente por su practicidad, estudiar los problemas como circuitos.
Fuerza magnetomotriz ($f_m$)($\mathcal{F}$)
\[\mathcal{F}=NI=\oint H\cdot d\]Semejanzas circuitos eléctricos - circuitos magnéticos
| Eléctrico | Magnético |
|---|---|
| $\sigma$ Conductividad | $\mu$ Permeabilidad $\left[\dfrac{H}{m}\right]$ |
| $E$ Intensidad de campo | $H$ Intensidad de campo $\left[\dfrac{Av}{m}\right]$ |
| $\mathrm{I}=\iint\vec{J}\cdot d\vec{s}$ Corriente | $\Phi=\iint \vec{B}\cdot d\vec{s}$ Flujo magnético [$Wb$] |
| $J=\dfrac{I}{s}=\sigma E$ Densidad de corriente | $B=\dfrac{\Phi}{s}=\mu H$ Densidad de flujo [$T$] |
| $V$($fem$) Fuerza electromotriz | $\mathcal{F}$ Fuerza magnetomotriz [$A$] |
| $R$ Resistencia | $\mathcal{R}$ Reluctancia [$H^{-1}$] |
| $G=\dfrac{1}{R}$ Conductancia | $\mathcal{P}=\dfrac{1}{\mathcal{R}}$ Permeancia [$H$] |
| Ley de Ohm: \(\displaystyle\left\{\begin{aligned}R&=\dfrac{V}{\mathrm{I}}=\dfrac{l}{\sigma s}\\V&=\mathrm{I}R=El\end{aligned}\right.\) | Ley de Ohm: \(\displaystyle\left\{\begin{aligned}\mathcal{R}&=\dfrac{\mathcal{F}}{\Phi}=\dfrac{l}{\mu s}\\\mathcal{F}&=\mathcal{\Phi}\mathcal{R}=Hl=N\mathrm{I}\end{aligned}\right.\) |
| Ley de Kirchoff: \(\displaystyle\left\{\begin{aligned}\Sigma\mathrm{I}&=0 \leftarrow Nodo\\\Sigma V -\Sigma R\mathrm{I}&=0 \leftarrow Malla\end{aligned}\right.\) | Ley de Kirchoff: \(\displaystyle\left\{\begin{aligned}\Sigma\Phi&=0 \leftarrow Nodo\\\Sigma \mathcal{F} -\Sigma \mathcal{R}\Phi&=0 \leftarrow Malla\end{aligned}\right.\) |