• Notas
• 6to Semestre
• Maquinas eléctricas

Máquinas de corriente continua

Compuesta por:

• Rotor: Se encarga de realizar la conversión de energía electromecánica. También se le conoce como Armadura o Inducido.
• Estator: Se utiliza para generar el campo magnético. También se le conoce como Devanado de campo o Inductor.

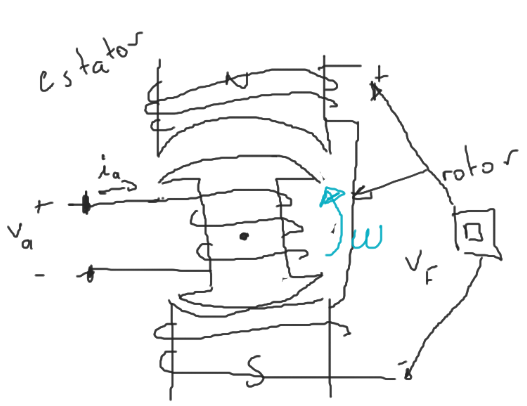
Modelo (circuito eléctrico equivalente)

Estator	Rotor

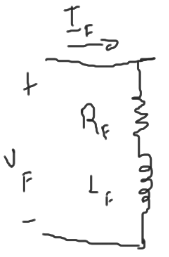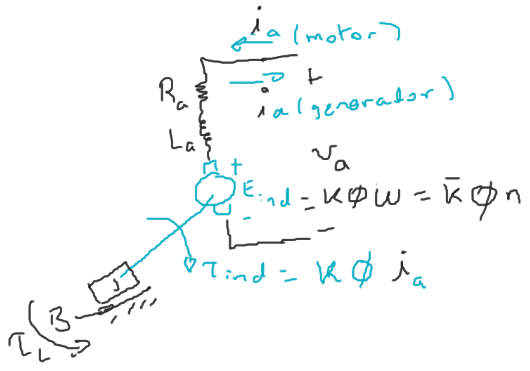Motor	Generador
$T_{ind}=T_L+B\omega$	$T_L=T_{ind}+B\omega$
$T_{ind} > T_L$	$T_L > T_{ind}$
$V_a > E_{ind}$	$E_{ind} > V_a$

Las pérdidas en el núcleo se determinan a partir de la prueba en vacío (sin carga).

La conversión de energía electromecánica:

\[E_{ind}\ i_a=T_{ind}\ \omega\]

Regulación de la velocidad (RV):

\[RV=\dfrac{n_{vacío}-n_{pc}}{n_{pc}}\times 100\]

Tipos de máquinas de C.C.

• Nota: Las variables en estado estacionario se muestran en mayúsculas y las del estado transitorio en minúsculas.

Excitación separada.

\[\newcommand{\dpartial}[2]{\dfrac{\partial#1}{\partial#2}} \newcommand{\derivate}[2]{\dfrac{d#1}{d#2}} \begin{cases} V_F=R_F I_F+L_F\cancel{\derivate{I_F}{t}}^0\\ V_a=R_a i_a+L_a\cancel{\derivate{i_a}{t}}^0+e_{ind} \end{cases}\]

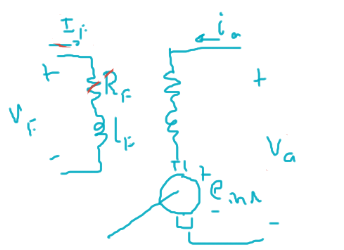
En el estado estacionario.

\[\begin{cases} V_F=R_F I_F\\ V_a=R_a I_a+E_{ind} = R_a I_a+K\Phi\omega \end{cases}\]

Por lo tanto, para controlar su velocidad:

\[\omega=\dfrac{V_a-R_a I_a}{K\Phi}\]

Se puede:

• Control por tensión: Variar la tensión de armadura $V_a$
• Control de campo: Variando el valor del campo $\Phi$
• Control por demanda de par: Variando el valor de la corriente de armadura $I_a$

Exitación en derivación (paralelo, shunt).

\[\begin{aligned} I_L&=I_a+I_F\\ V_a&=V \end{aligned}\]

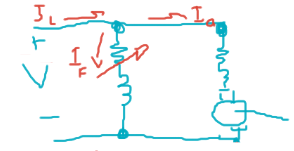
Exitación en serie.

\[E_{ind} = V - (R_F + R_A) I\]

Para circuito magnético lineal o no saturado.

\[\phi = c I\quad,\quad c = cte.\] \[\begin{aligned} E_{ind} &= K\phi\omega = K c I \omega\\ &= K_v I \omega\\ \end{aligned}\]

Donde:
$K_v$ = Constante de tensión $[\dfrac{V}{A\ rad/s}]$

\[\tau_{ind} = K\phi I= K c I I = K_t I^2\\\]

Donde:
$K_t$ = Constante de par $[\dfrac{N m}{A^2}]$
Sustituyendo $E_{ind}$:

\[K_v I \omega = V - (R_F + R_A) I\\\] \[I = \sqrt{\dfrac{\tau_{ind}}{K_t}}\]

Por lo tanto:

\[\omega = \dfrac{V}{\sqrt{K_v}}\dfrac{1}{\sqrt{\tau_{ind}}} - \dfrac{(R_F + R_A)}{K_v}\\\]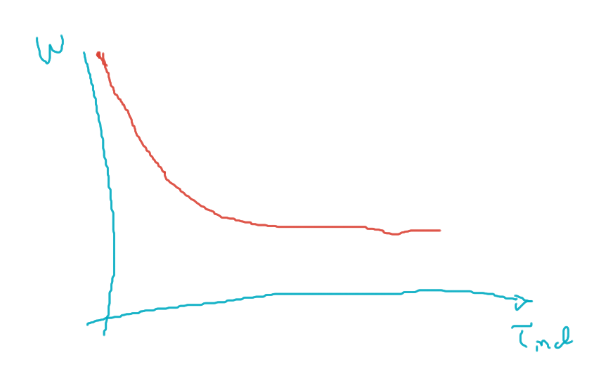

Exitación de imanes permanentes.

Ejercicios

Los ejercicios 1 al 5 se refieren al motor conectado en derivación con las siguientes características.

$P_{\text{nominal}}=15\ hp$	$I_{L\text{nominal}}=55 A$
$V_T=240V$	$n_\text{nominal}=1200\ rpm$
$100 \leq R_\text{ajustable} \leq 400 \Omega$

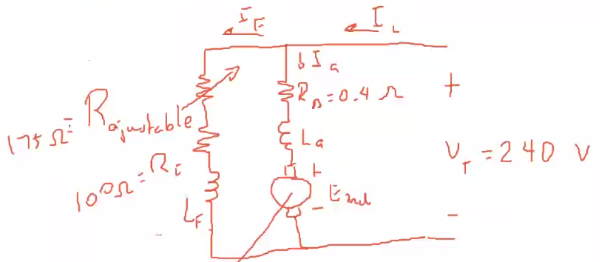
Ejercicio 1

Si $R_{\text{ajustable}}= 175\Omega$, ¿cuál es la velocidad de rotación del motor en condiciones de vacío $n_{\text{vacío}}$?

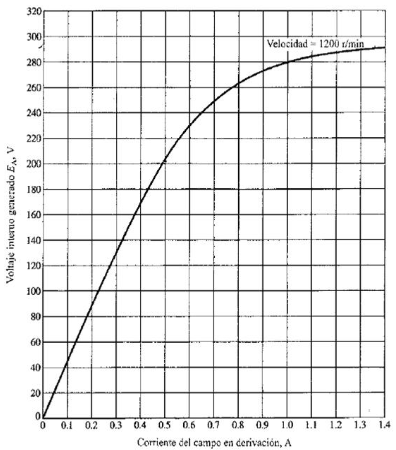
\[E_{ind}=K\Phi \omega = \bar{K}\Phi n\\\] \[\begin{aligned} I_F &= \dfrac{V_T}{R_{\text{ajustable}}+R_I}=\dfrac{240}{175+100}\\ &=0.87A \end{aligned}\] \[I_F = 0.87 \xRightarrow{curva}\begin{cases} E_{ind}=275 V\\ n = 1200\ rpm \end{cases}\]

En vacio:

\[\boxed{I_a=0}\] \[\boxed{E_\text{vacío}=V_T=240V}\] \[\boxed{\dfrac{E_{ind}}{E_\text{vacío}}=\dfrac{\cancel{\bar{K}\Phi}\ n}{\cancel{\bar{K}\Phi}\ n_\text{vacío}}}\]

Por lo tanto:

\[\newcommand{\result}[1]{\underline{#1/}} \begin{aligned} n_\text{vacío}&=\dfrac{n E_\text{vacío}}{E_{ind}}=\dfrac{1200\ rpm(240 V)}{275 V}\\ &=\result{1047\ rpm} \end{aligned}\]

Ejercicio 2

Si no existe reacción del inducido, ¿cuál es la velocidad del motor a plena carga? ¿cuál es la regulació́n de velocidad del motor? ¿cuál es la curva de velocidad - par del motor?

\[\tag{1} \dfrac{E_{ind}}{E_{pc}}=\dfrac{\bar{K}\phi n}{\bar{K}\phi n_{pc}}=\dfrac{n}{n_{pc}}\]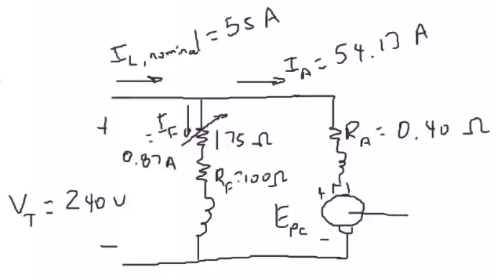

\[I_L = I_A + I_F\quad\Rightarrow\quad I_A = 54.1\] \[\boxed{\begin{matrix}I_L\approx I_F\\I_A\approx0\end{matrix}\quad \text{vacío}}\] \[\boxed{ \begin{matrix} I_L\approx I_A\\ I_F \ll I_A \end{matrix}\quad \text{plena carga} }\]

Aplicando LVK:

\[V_T=R_AI_A + E_{pc}\\ \begin{aligned} E_{pc}&= V_T -R_AI_A=240-0.4(53.13)\\ &=218.34V \end{aligned}\] \[I_F = 0.87A \xRightarrow{curva}\begin{cases} E_{ind}=275 V\\ n = 1200\ rpm \end{cases}\]

Sustituyendo en (1):

\[\newcommand{\result}[1]{\underline{#1/}} n_{pc}=\dfrac{1200(218.34)}{275}=\result{953\ rpm}\]

Del ejercicio 2, sabemos que $n_{vacío}=1047\ rpm$

\[\newcommand{\result}[1]{\underline{#1/}} RV=\dfrac{1047 - 953}{953}\times100\%=\result{9.68\%}\] \[V_T= R_AI_A + E_{ind}=R_AI_A+K\phi\omega\] \[\omega=\dfrac{V_T}{K\phi}-\dfrac{R_AI_A}{K\phi}\ldots(2)\] \[\tau_{ind}=K\phi I_A\] \[I_A=\dfrac{\tau_{ind}}{K\phi I_A}\ldots(3)\]

Sustituyendo (3) en (2):

\[\omega=\dfrac{V_T}{K\phi}-\dfrac{R_A\tau_{ind}}{(K\phi)^2}\quad\leftarrow\quad\text{curva par - velocidad}\]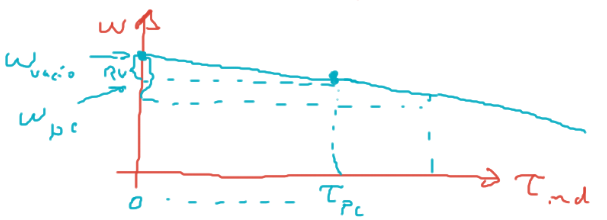

Ejercicio 3

Si el motor está operando a plena carga y su resistencia variable se aumenta a 250 Ω?, ¿cuál es la nueva velocidad del motor, RV, $n_{vacío}$?

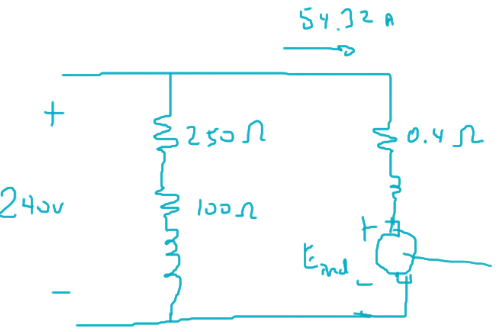
En el vacio:

\[\boxed{\begin{matrix}I_L\approx I_F\\I_A\approx0\end{matrix}\quad \text{vacío}}\] \[I_F=\dfrac{240}{250+100}=0.68\] \[I_F = 0.68A \xRightarrow{curva}\begin{cases} E_{ind}=248 V\\ n = 1200\ rpm \end{cases}\] \[V_T=E_{vacío}=240V\] \[\dfrac{E_{ind}}{E_{vacío}}=\dfrac{n}{n_{vacío}}\] \[\newcommand{\result}[1]{\underline{#1/}} n_{vacío}=\dfrac{E_{vacío}n}{E_{ind}}=\result{1161\ rpm}\]

Con plena carga:

\[I_L=55A,\quad I_F=0.68A\quad\Rightarrow\quad I_A=54.32A\] \[E_{pc}= V_T -R_AI_A=240-0.4(54.32)=218.27V\\\] \[\dfrac{E_{ind}}{E_{pc}}=\dfrac{n}{n_{pc}}\] \[\newcommand{\result}[1]{\underline{#1/}} n_{pc}=\dfrac{E_{pc}n}{E_{ind}}=\result{1056\ rpm}\] \[\newcommand{\result}[1]{\underline{#1/}} RV=\dfrac{1047 - 953}{953}\times100\%=\result{9.9\%}\]

Ejercicio 4

Si la resistencia variable puede ser ajustada de 100 a 400 Ω?, ¿cuáles son las velocidades máxima y mínima de estemotor en vacío y a plena carga?

Con $R_{ajustable}= 400Ω$

En el vacio:

\[\boxed{\begin{matrix}I_L\approx I_F\\I_A\approx0\end{matrix}\quad \text{vacío}}\] \[I_F=\dfrac{240}{400+100}=0.48\] \[I_F = 0.48A \xRightarrow{curva}\begin{cases} E_{ind}=198 V\\ n = 1200\ rpm \end{cases}\] \[V_T=E_{vacío}=240V\] \[\newcommand{\result}[1]{\underline{#1/}} n_{vacío}=\dfrac{E_{vacío}n}{E_{ind}}=\result{1454\ rpm}\]

Con plena carga:

\[I_L=55A,\quad I_F=0.48A\quad\Rightarrow\quad I_A=54.52A\] \[E_{pc}= V_T -R_AI_A=240-0.4(54.52)=218.19\\\] \[\newcommand{\result}[1]{\underline{#1/}} n_{pc}=\dfrac{E_{pc}n}{E_{ind}}=\result{1322\ rpm}\] \[\newcommand{\result}[1]{\underline{#1/}} RV=\dfrac{1047 - 953}{953}\times100\%=\result{9.98\%}\]

Con $R_{ajustable}= 100Ω$

En el vacio:

\[\boxed{\begin{matrix}I_L\approx I_F\\I_A\approx0\end{matrix}\quad \text{vacío}}\] \[I_F=\dfrac{240}{100+100}=1.2\] \[I_F = 1.2A \xRightarrow{curva}\begin{cases} E_{ind}=288 V\\ n = 1200\ rpm \end{cases}\] \[V_T=E_{vacío}=240V\] \[\newcommand{\result}[1]{\underline{#1/}} n_{vacío}=\dfrac{E_{vacío}n}{E_{ind}}=\result{1000\ rpm}\]

Con plena carga:

\[I_L=55A,\quad I_F=1.2A\quad\Rightarrow\quad I_A=53.8A\] \[E_{pc}= V_T -R_AI_A=240-0.4(53.8)=218.48\\\] \[\newcommand{\result}[1]{\underline{#1/}} n_{pc}=\dfrac{E_{pc}n}{E_{ind}}=\result{910\ rpm}\] \[\newcommand{\result}[1]{\underline{#1/}} RV=\dfrac{n_{vacío}-n_{pc}}{n_{pc}}\times100\%=\result{9.89\%}\]

Ejercicio 5

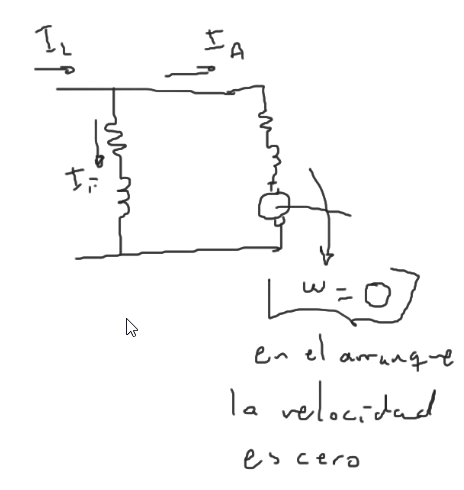
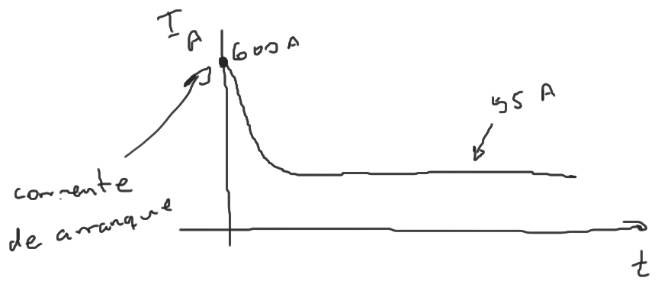
¿Cuál es la corriente de arranque de esta máquina, si arranca conectándola directamente a VT. Comparar esta corriente de arranque con la corriente nominal del motor.

\[\begin{aligned} V_T&=R_AI_A + E_{ind}\\ &=R_AI_A + K\phi\cancel{\omega}\\ \end{aligned}\] \[\newcommand{\result}[1]{\underline{#1/}} I_{A, Arranque}=\dfrac{V_T}{R_A}=\dfrac{240}{0.4}=\result{600A}\]

\[I_{A,arranque}\gg I_F\\ \therefore\ I_{A,arranque}=T_{L,arranque}=I_{arranque}\] \[\newcommand{\result}[1]{\underline{#1/}} \dfrac{I_{arranque}}{I_{nominal}}=\dfrac{600}{55}=\result{10.9}\]