Transformadores
En la figura siguiente se muestra un transformador ideal, que se compone del devanado primario (alimentación) y el secundario.
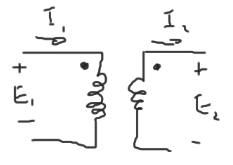
Relación de transformación $a$
La relación de transformación se define como:
Sin embargo, esto no es una forma práctica para poder calcularlo. Por eso en la práctica se utiliza lo siguiente:
\[S_\text{entrada} = S_\text{salida}\]$S$ = Potencia aparente [$VA$]
\[E_1I_1 = E_2I_2\] \[\dfrac{E_1}{E_2} = \dfrac{I_2}{I_1}\]Por lo tanto:
\[\boxed{a = \dfrac{N_1}{N_2} = \dfrac{I_2}{I_1} = \dfrac{E_1}{E_2}}\]Conociendo $a$, podemos conocer los valores del otro lado.
Impedancia $Z$
Se define una impedancia:
Por lo tanto:
\[Z_2=\dfrac{E_2}{I_2}\] \[\begin{aligned} Z_1&=\dfrac{E_1}{I_1}=\dfrac{aE_2}{\dfrac{I_2}{a}}= a^2\dfrac{E_2}{I_2} = a^2Z_2\\ &=a^2(R_2+jX_2) \end{aligned}\]Modelo del transformador
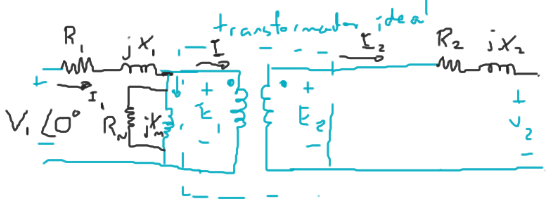
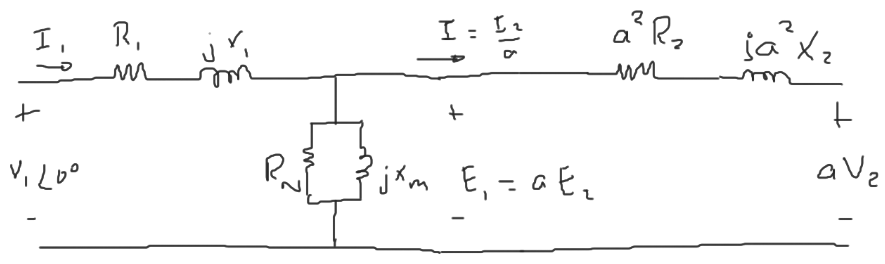
Donde:
$R_1$ = Resistencia del primario [$\Omega$]
$X_1$ = Reactancia inductiva del primario [$\Omega$]
$R_2$ = Resistencia del secundario [$\Omega$]
$X_2$ = Reactancia inductiva del secundario [$\Omega$]
$X_m$ = Reactancia de magnetización.
$R_N$ = Representa las pérdidas en el núcleo (se determinan haciendo una prueba al vacío).
Donde:
$f$ = Frecuencia eléctrica [Hz].
Para determinar de forma experimental las resistencias del primario o secundario se realiza la prueba de corriente directa.
Para determinar de forma experimental las reactancias se utiliza la prueba de corto circuito.
La tensíon inducida en el secundario $E_2$, se cálcula con la Ley de Faraday:
Potencia de entrada
\[P_\text{entrada} = V_1 I_1 \cos{\theta}\]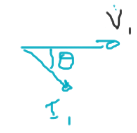
Donde:
$cos\theta = f.p. =$ Factor de potencia.
Factor de potencia
\[\begin{cases} f.p. > 1 & \text{Carga capacitiva}\\ f.p. = 1 & \text{En fase}\\ f.p. < 1 & \text{Carga inductiva}\\ \end{cases}\]En las industrias, el factor de potencia no puede ser menor a 0.8.
Potencia aparente
\[S_\text{aparente} = V_1 I_1 [VA]\]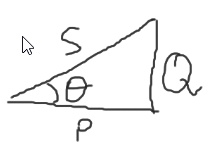
Eficiencia de un transformador
\[\eta = \dfrac{P_\text{salida}}{P_{entrada}}\]Pérdidas en el devanado primario
\[P_{DP} = |I_1|^2 R_1\]Pérdidas en el núcleo
\[P_\text{Núcleo} = \dfrac{|E_1|^2}{R_N}\]Pérdidas en el devanado primario
\[P_{DS} = |I_2|^2 R_2\]Potencia de salida
\[\begin{aligned} P_\text{salida} &= |V_2||I_2|\cos{\theta_2}\\ &= P_\text{entrada} - P_{DP} - P_\text{Núcleo} - P_{DS} \end{aligned}\]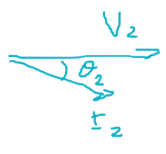
Circuito equivalente referido al primario