Análisis de sistemas en variables de estado

Sistemas lineales y no lineales

Sistemas lineales y no lineales

Un sistema lineal sólo puede tener estos 3 comportamientos:

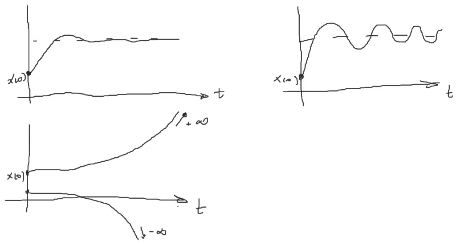
Los sistemas no lineales

Teorema de superposición

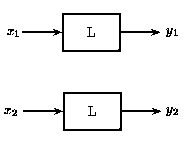
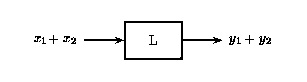
Principio de homogeneidad

Linealidad de los sistemas

Un sistema es lineal si cumple el Teorema de Superposición y el Principio de homogeneidad. En otro caso el sistema es no lineal.

Ejercicios: Demostrar si $y=f(x)$ es lineal o no lineal

$y = x + 2$

\[\begin{aligned} y(x_1) &= x_1 + 2\\ y(x_2) &= x_2 + 2\\ y(x_1) + y(x_2) &= x_1 + x_2 + 4\\ y(x_1 + x_2) &= x_1 + x_2 + 2 \neq y(x_1) + y(x_2) \end{aligned}\]

Por lo tanto, no es lineal

$y = x^2$

\[\begin{aligned} y(x_1) &= x_1^2\\ y(x_2) &=x_2^2\\ y(x_1) + y(x_2) &=x_1^2 + x_2^2\\ y(x_1 + x_2) &= (x_1 + x_2)^2 \end{aligned}\]

Por lo tanto, no es lineal

$y=sen(x)$

\[\begin{aligned} y(x_1) &= \sin{x_1}\\ y(x_2) &=\sin{x_2}\\ y(x_1) + y(x_2) &=\sin{x_1} + \sin{x_2}\\ y(x_1 + x_2) &= \sin(x_1 + x_2) \end{aligned}\]

Por lo tanto no es lineal

$y=ax$

\[\begin{aligned} y(x_1) &= ax_1\\ y(x_2) &= ax_2\\ y(x_1) + y(x_2) &= ax_1 + ax_2\\ y(x_1 + x_2) &= a(x_1 + x_2) = ax_1 + ax_2 \end{aligned}\] \[\begin{aligned} y(x) &= ax\\ y(\alpha x) &= a\alpha x = \alpha a x\\ &= \alpha y(x) \end{aligned}\]

Por lo tanto, sí es lineal

Ejercicios: Demostrar si las ecuaciones diferenciales son lineales o no lineales

Otra forma de ver si el sistema es lineal o no, es por medio de la ecuación general de estado.

$\dot{y} + 2 y = 0$ Sí es lineal porque $2 y$ y $\dot{y}$ cumplen con superposición y con homogeneidad
$\ddot{y} + y\dot{y} = 0$ No es lineal

\[y(x_1)\dot{y}(x_1) + y(x_2)\dot{y}(x_2) \neq [y(x_1)+y(x_2)][\dot{y}(x_1)+\dot{y}(x_2)]\\\]

Forma general de un sistema lineal

Un sistema lineal con una entrada y una salida tiene la siguiente forma,

\[y^{(n)} + a_1y^{(n-1)} + a_2y^{(n-2)} + \ldots + a_ny = u\]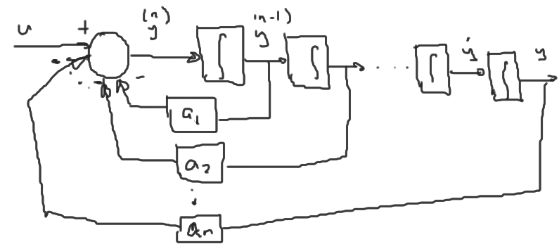

Representación de espacio de estado

\[\begin{aligned} x_1 &= y\\ x_2 &= \dot{y} = \dot{x_1}\\ x_3 &= \ddot{y} = \dot{x_2}\\ &\vdots\\ x_n &= \ddot{y} = \dot{x_{n-1}}\\ \dot{x_n} &= y^n = -a_ny - a_{n-1}\dot{y} - \ldots - a_2y^{(n-2)} - a_1y^{(n-1)} + u\\ \dot{x_n} &= -a_nx_1 - a_{n-1}x_2 - \ldots - a_2x_{n-1} - a_1x_{n} + u\\ \end{aligned}\]

Pasandolo a forma matricial:

\[\begin{cases} \dot{x} &= Ax + Bu\\ y &= Cx \end{cases}\quad,\quad x(0) = x_0\]

Donde
$x: n\times1$, $A:n\times n$, $u:m\times 1$, $B:n\times m$,$y:p\times 1$, $C: p\times n$

Ejemplo

$\ddot{y} + 4\dot{y} + 3y = u$

$x_1 = y$
$x_2 = \dot{y} = \dot{x_1}$
$\dot{x_2} = \ddot{y} = -3y - 4\dot{y}+u$

Por lo tanto:

\[\begin{cases} \dot{x_1} = x_2\\ \dot{x_2} = -3x_1-4x_2 + u\\ \end{cases}\] \[\begin{aligned} \dot{x} &= \begin{bmatrix} 0&1\\ -3&-4\\ \end{bmatrix}x + \begin{bmatrix}0\\1\end{bmatrix}u\\ y &= \underbrace{\begin{bmatrix}1&0\end{bmatrix}}_{C}x \end{aligned}\]