Controlabilidad y observabilidad de sistemas lineales
En un sistema en representación de variables de estado:
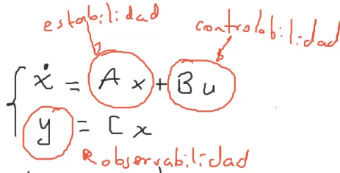
Donde:
$x$ = Vector de estado
$u$ = Entrada
$y$ = Salida
Controlabilidad
La controlabilidad se refiere a la existencia de una entrada $u$ para controlar cada variable de estado de manera independiente.
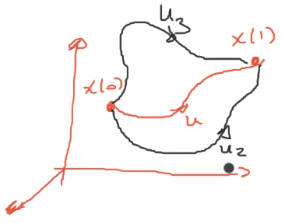
El sistema
\[\begin{cases} \dot{x} &= Ax + Bu\\ y &= Cx \end{cases}\]Tambien llamdo el par $(A,B)$ es controlable sí para todo estado inicial $x(0)=x_0$ y el estado final $x_1=x(T)$, existe una entrada $u(t)$ que lleva al sistema de $x_0$ a $x_1$ en tiempo finito $t:[0,T]$.
En otro caso, se dice que no es controlable.
Se evalúa variando la entrada y si cambian las variables de estado, es controlable.
Criterios para determinar la controlabilidad
Criterio de Kalman
La matriz de controlabilidad
\[\mathcal{C} = [B\ AB\ A^2B\ \ldots\ A^{n-1}\ B]\quad:\quad n\times nm\]es de rango completo
\[\text{rango}(C) = n\]rank(C)
Si el sistema tiene una entrada ($m=1$) entonces:
\[\det(C)\neq 0\]Criterio de Hautus
La matriz de controlabilidad
\[H_c = [\lambda I-A, B]\quad:\quad n\times(n+m)\]es de rango completo, para todo $\lambda \in \mathbb{C}$
\[\text{rango}(H_c) = n\]Criterio 3
Los valores propios de la matriz $A-BK$ pueden asignarse arbitrariamente mediante la selección apropiada de $K$.
\[u = -kx\] \[\dot{x} = Ax + Bu = Ax - BKx = (A-BK)x\]Ejemplo
Calcular $K$ para que $(A-BK)$ tenga valores propios $-2$ y $-3$.
a).
Por lo tanto
\[K_1 = 5\\ K_1 = 7\\\]Así que no es controlable puesto que la solución no es única
b).
\[\dot{x} = \begin{bmatrix} 1&-1\\ 0&-1\\ \end{bmatrix}x + \begin{bmatrix} 0\\1 \end{bmatrix}u\]Se encuentra:
\[s^2 + K_2 + s - K_1 - K_2 - 1 = S^2+5s+6\] \[\begin{aligned} K_2 &= 5\\ K_1 &= -5-1-6 = -12\\ \end{aligned}\]Por lo tanto el resultado es único y el sistema es controlable.
Criterio 4 Gramiano
\[G_c(t) = \int_0^t e^{A\tau} BB^Te^{A^T\tau}d\tau\]es invertible si
\[\det(G_c(t))\neq0\]gram(sys,'c') <-- Controlabilidad
Observabilidad
La observabilidad consiste en determinar si el estado inicial puede ser aproximado (calculado, reconstruido ,estimado, observado) conociendo $y(t)$.
Se evalúa variando las $c.i.$ y si cambia la salida es observable.
Criterios para determinar observabilidad
Sea el sistema
\[\begin{cases} \dot{x} &= Ax + Bu\\ y &= Cx \end{cases}\quad,\quad x(0) = x_0\]El par $A$, $C$ es observable si cumple con alguno de los siguientes criterios:
Criterio de Kalman
La matriz de observabilidad
\[O = \begin{bmatrix}C\\CA\\CA^2\\\vdots\\CA^{n-1}\end{bmatrix}\]Donde $O$ es de tamaño $np\times n$ y es de rango completo $\text{rango}(O) = n$.
Si el sistema sólo tiene una salida ($p = 1$):
Si el rango es igual al orden del sistema $n$, entonces el sistema es observable.
Criterio de Hautus
La matriz de observabilidad
\[H_O = \begin{bmatrix}LI-A\\C\end{bmatrix}\]Donde $L$ son los valores propios de A.
Determina que el sistema es observable si el rango de $H_O$ es máximo (igual al órden del sistema $n$) para todos los valores de $L$.
Criterio 3
Los valores propios de la matriz $A-LC$ pueden asignarse arbitrariamente mediante la selección apropiada de $L$.
Criterio 4 Gramiano
\[G_o(t) = \int_0^t e^{A^T\tau} C^TC e^{A\tau}d\tau\]es invertible para todo $t \geq 0$ si
\[\det(G_o)\neq0\]gram(sys,'o') <-- Observabilidad
Ejemplos
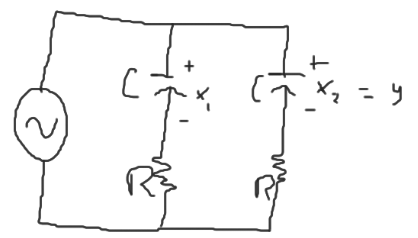
Indicar si las variables en los siguientes sistemas son controlables y observables a partir de un análisis en simulación.
-
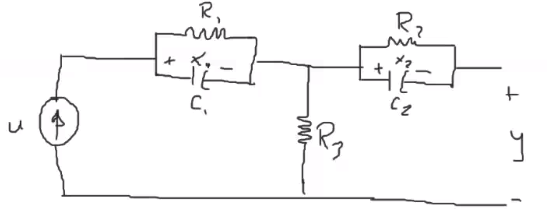
Haciendo el análisis en matlab, se determina que el sistemano es controlabley no es observable 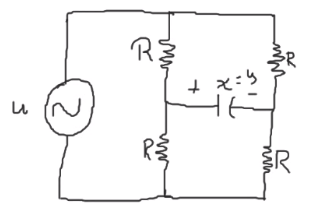
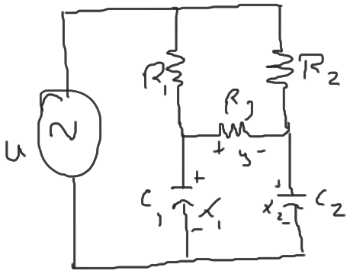
- No es controlable
- Sí es observable
-