• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

Discretización de ecuaciones en espacio de estado

Considere el sistema en tiempo continuo,

\[\tag{1}\begin{aligned} \dot{x}(t) &= Ax(t) + Bu(t)\\ y(t) &= Cx(t) \end{aligned}\]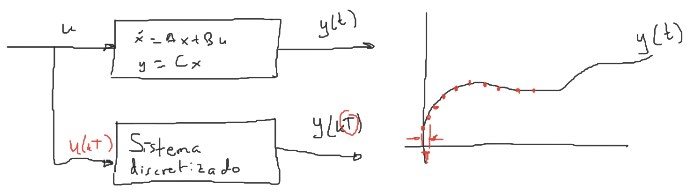

La solución del sistema $(1)$ está dada por,

\[\tag{2} x(t) = \mathcal{L}^{-1}\left\{(sI-A)^{-1}\right\}x(0) + \mathcal{L}^{-1}\left\{(sI-A)^{-1}Bu(s)\right\}\] \[\tag{3} x(t) = e^{At}x(0) + \int_0^t e^{A(t-\tau)}Bu(\tau)d\tau\]

Se busca llevar el sistema $(1)$ a un sistema en tiempo discreto de la siguiente forma:

\[\begin{aligned} \dot{x}((k+1)T) &= \overline{A}x(kT) + \overline{B}u(kT)\\ y(kT) &= Cx(kT) \end{aligned}\]

Para hacer la sustitución $t = kT$ en la solución del sistema, se utiliza la ecuación $(3)$:

\[\tag{4} x(kT) = e^{AkT}x(0) + e^{AkT}\int_0^{kT} e^{-A\tau}Bu(\tau)d\tau\]

Haciendo $t = (k+1)T$

\[\tag{5} x((k+1)T) = e^{A(k+1)T}x(0) + e^{A(k+1)T}\int_0^{(k+1)T} e^{-A\tau}Bu(\tau)d\tau\]

Multiplicando $(4)$ por $e^{At}:n\times n$

\[\tag{6} e^{AT} x(kT) = e^{A(k+1)T}x(0) + e^{A(k+1)T}\int_0^{kT} e^{-A\tau}Bu(\tau)d\tau\]

Restando $(5) - (6)$:

\[\begin{aligned} x((k+1)T) - e^{AT}x(kT) &= e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}Bu(\tau)d\tau\\ x((k+1)T) &= \underbrace{e^{AT}}_{\overline{A}}x(kT) + e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}Bu(\tau)d\tau\\ \end{aligned}\]

Para $u(kT) = cte.$ para $kT \leq t \leq (k+1)T$

entonces:

\[\tag{7} x((k+1)T) = \underbrace{e^{AT}}_{\overline{A}}x(kT) + \underbrace{\left(e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}d\tau\right)B}_{\overline{B}}u(kT)\]

El sistema se aproxima escalonadamente:

Como se puede observar, depende de $T$ el error que se tenga, a menor $T$, mejor error.

Ahora bien, asumiendo que $A$ es invertible:

\[\tag{8} \begin{aligned} e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}d\tau &= e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}\underbrace{A^{-1}A}_{I}\ d\tau\\ &= e^{A(k+1)T}\left[-e^{-A\tau} A^{-1}\right]_{kT}^{(k+1)T} = \\ &= \left[-I + e^{AT}\right]A^{-1} \end{aligned}\]

Haciendo $k = 0$ en $(8)$

\[\begin{aligned} e^{AT}\int_0^T e^{-A\tau}d\tau &= e^{AT}\left[-e^{-A\tau}A^{-1}\right]_0^T = e^{AT}\left[-e^{-A\tau}A^{-1} + e^0A^{-1}\right]_0^T\\ &= \left[-I + e^{AT}\right]A^{-1} \end{aligned}\]

Se puede ver que si $A$ es invertible, no depende del instante de muestreo $k$.

De $(7)$,

\[x((k+1)T) = \underbrace{e^{AT}}_{\overline{A}}x(kT) + \underbrace{\left(e^{A(k+1)T}\int_{kT}^{(k+1)T}e^{-A\tau}d\tau\right)}_{\int_0^T e^{-A(T-\tau)}d\tau}Bu(kT)\]

Se define

\[\begin{cases} \lambda = T - \tau\\ d\lambda = -d\tau \end{cases}\quad\Rightarrow\quad\text{si}\quad\begin{array}{c} \tau = 0 \Rightarrow \lambda = T\\ \tau = T \Rightarrow \lambda = 0\\ \end{array}\]

Así

\[\int_0^T e^{-A(T-\tau)}d\tau = -\int_T^0e^{-A\lambda}d\lambda = \int_0^Te^{-A\lambda}d\lambda\]

De forma que

\[\begin{aligned} \overline{A}(T) &= e^{AT}\\ \overline{B}(T) &= \left(\int_0^Te^{-A\lambda}d\lambda\right)B\\ \end{aligned}\] \[\boxed{ \begin{aligned} \dot{x}((k+1)T) &= \overline{A}x(kT) + \overline{B}u(kT)\\ y(kT) &= Cx(kT) \end{aligned} }\]

Ejercicio

1. Sea el sistema SISO,

   \[\tag{1}\begin{cases} \dot{x}(t) = -2x(t) + 3u(t)\\ y(t) = x(t) \end{cases}\]

   Discretizar el sistema $(1)$ para:

   1. $u(t) = 1$
   2. $u(t) = \sin(t)$
   \[\overline{A}(T) = e^{AT} = e^{-2T}\] \[\overline{B}(T) = \left(\int_0^T e^{A\lambda}d\lambda\right)B = \left(\int_0^T e^{-2\lambda}d\lambda\right)3 = -\frac{3}{2}e^{-2\lambda}\vert_0^T = -\frac{3}{2}e^{-2T} + \frac{3}{2}\]

   Por lo tanto:

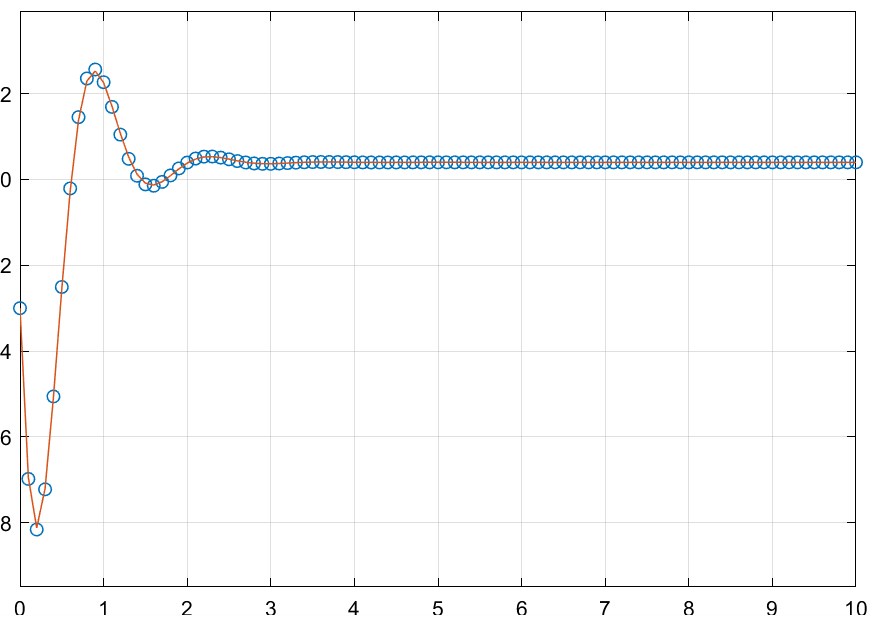
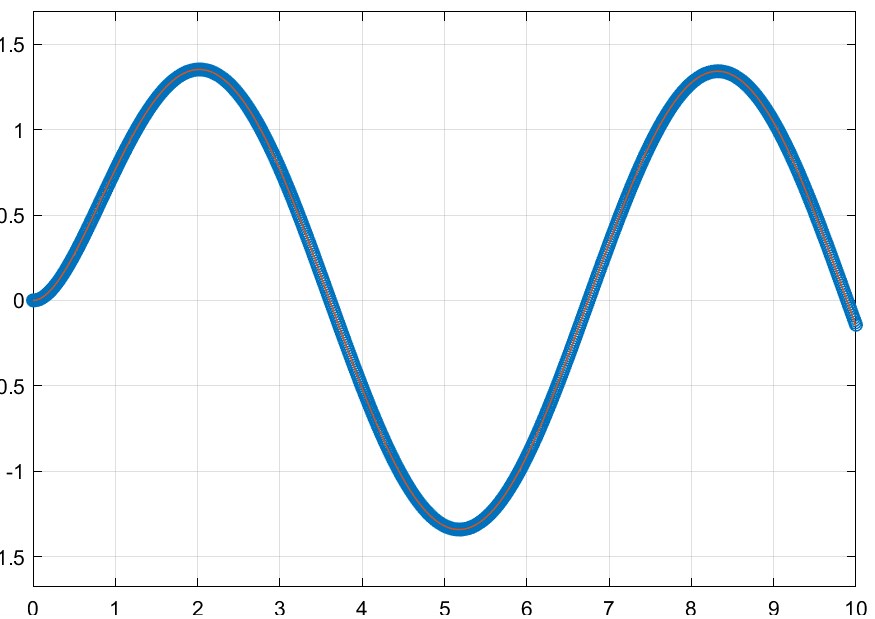
   \[\tag{2}\begin{cases} x((k+1)T) = e^{-2T}x(kT) + \frac{3}{2}(1 - e^{-2T})u(kT)\\ y(kT) = x(kT) \end{cases}\]

   Simulando los sistemas $(1)$ y $(2)$ para $u(t) = 1$,$T=0.2$ y $u(t) = \sin(t)$,$T = 0.02$ respectivamente, se obtiene el siguiente resultado:

   

   

2. Discretizar el sistema

   \[\tag{1}\begin{cases} \dot{x}(t) = \begin{bmatrix} 0 & 1\\ -25 & -4 \end{bmatrix}x(t) + \begin{bmatrix} 0\\1 \end{bmatrix}u(t)\\ y(t) = \begin{bmatrix} 1 & -1 \end{bmatrix}x(t) \end{cases}\]

   Discretizar el sistema $(1)$ para:

   1. $u(t) = 10$
   2. $u(t) = t$
   3. $u(t) = \sin(t)$

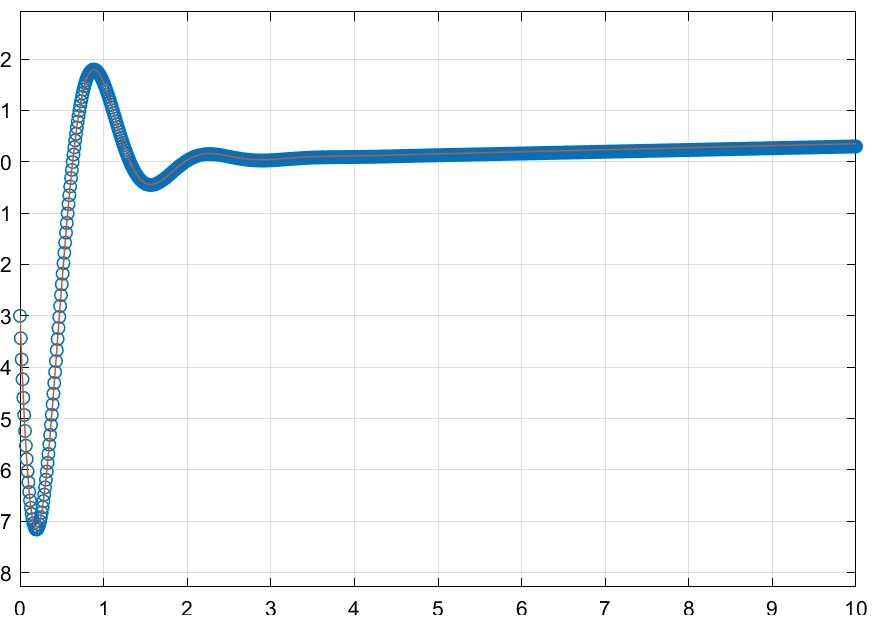
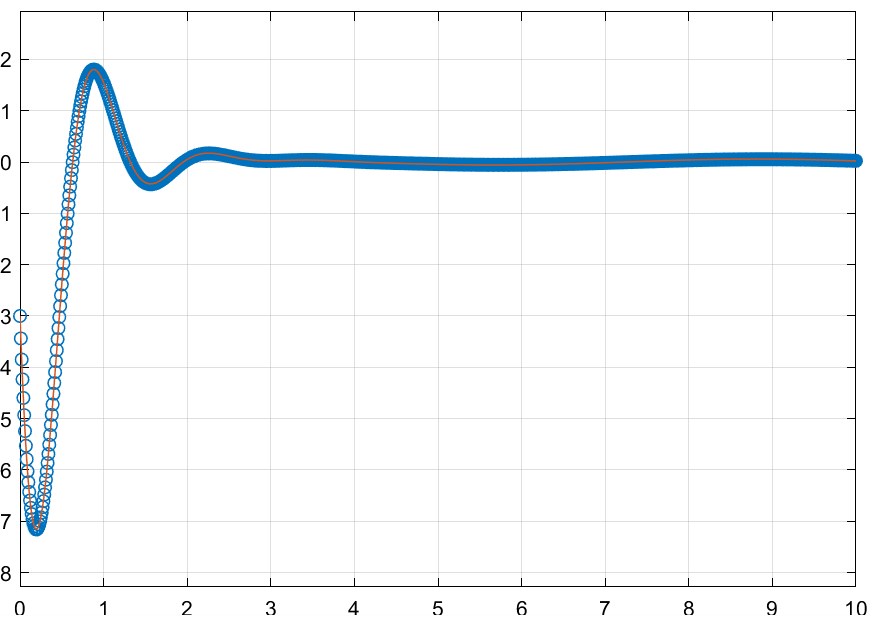
   Los valores de $\overline{A}$ y $\overline{B}$ se estiman con el comando de matlab [Ab,Bb] = c2d(A,B,T):

    A = [0   1
        -25 -4];
    B = [0
         1];
            
    T = 0.1; % este valor cambia por cada entrada
            
    [Ab,Bb] = c2d(A,B,T)
   

   Simulando los sistemas $(1)$ y $(2)$ para $u(t) = 10$,$T=0.1$ y $u(t) =\sin(t),u(t) = t$,$T = 0.01$ , se obtiene el siguiente resultado: