• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

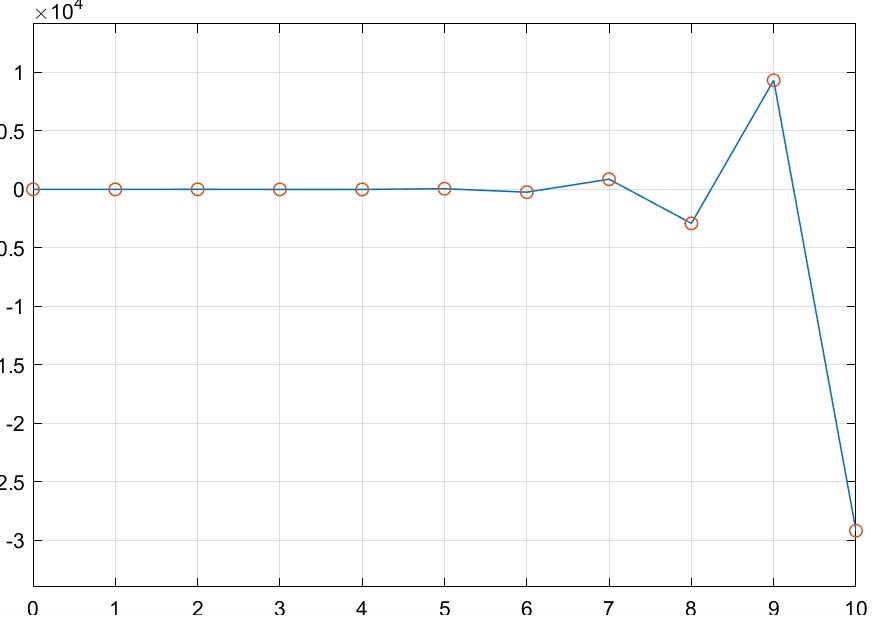
Forma canónica observable en tiempo discreto

Considere un sistema con función de transferencia,

$\frac{Y(z)}{U(z)} = \frac{b_1z^{-1} + b_2z^{-2} + \ldots + b_nz^{-n}}{1 + a_1z^{-1} + a_2z^{-2} + \ldots + a_nz^{-n}}$ $Y(z) + a_1z^{-1}Y(z) + a_2z^{-2}Y(z)+\ldots+a_nz^{-n}Y(z) = b_1z^{-1}U(z) + \ldots + b_nz^{-n}U(z)$ $Y(z) = z^{-1}\left[b_1 U(z) - a_1Y(z)\right] + z^{-2}\left[b_2U(z) - a_2Y(z)\right] + \ldots + z^{-n+1} \left[b_{n-1}U(z) - a_{n-1}Y(z)\right] + z^{-n}\left[b_nU(z) - a_{n}Y(z)\right]$ $Y(z) = z^{-1}\left[b_1U(z) - a_1Y(z) + z^{-1}\left\{b_2 U(z) - a_2Y(z) + \ldots + z^{-1}\left(b_{n-1} U(z) - a_{n-1}Y(z) + z^{-1}\left[b_n U(z) - a_n Y(z)\right]\right)\right\}\right]$

Se definen las variables de estado,

$\tag{a}\begin{cases} \begin{aligned} X_1(z) &= z^{-1}\left[b_nU(z) - a_nX_n(z)\right]\\ X_2(z) &= z^{-1}\left[b_{n-1}U(z) - a_{n-1}X_n(z) + X_1(z)\right]\\ &\vdots\\ X_{n-1}(z) &= z^{-1}\left[b_2U(z) - a_2X_n(z) + X_{n-2}(z)\right]\\ X_n(z) &= z^{-1}\left[b_1U(z) - a_1X_n(z) + X_{n-1}(z)\right] = Y(z)\\ \end{aligned} \end{cases}$

Multiplicando ambos lados del sistema $a$ por $z$:

$\tag{b}\begin{cases} \begin{aligned} zX_1(z) &= \left[b_nU(z) - a_nX_n(z)\right]\\ zX_2(z) &= \left[b_{n-1}U(z) - a_{n-1}X_n(z) + X_1(z)\right]\\ &\vdots\\ zX_{n-1}(z) &= \left[b_2U(z) - a_2X_n(z) + X_{n-2}(z)\right]\\ zX_n(z) &= \left[b_1U(z) - a_1X_n(z) + X_{n-1}(z)\right]\\ Y(z) &= X_n(z) \end{aligned} \end{cases}$

Aplicando la transformada inversa al sistema $b$:

$\tag{c}\begin{cases} \begin{aligned} x_1(k+1) &= - a_nx_n(k) + b_nu(k) \\ x_2(k+1) &= x_1(k) - a_{n-1}x_n(k) + b_{n-1}u(k) \\ &\vdots\\ x_{n-1}(k+1) &= x_{n-2}(k) - a_2x_n(k) + b_2u(k)\\ x_n(k+1) &= x_{n-1}(k) - a_1x_n(k) + b_1u(k)\\ y(k) &= x_n(k) \end{aligned} \end{cases}$

En forma matricial:

$\underbrace{\begin{aligned} x(k+1) &= \begin{bmatrix} 0 & 0 & 0 & \ldots & 0 & -a_n\\ 1 & 0 & 0 & \ldots & 0 & -a_{n-1}\\ 0 & 1 & 0 & \ldots & 0 & -a_{n-2}\\ \vdots & & \ddots & & \vdots & \vdots\\ 0 & 0 & \ldots & 1 & 0 & -a_{2}\\ 0 & 0 & \ldots & 0 & 1 & -a_{1}\\ \end{bmatrix}x(k) + \begin{bmatrix} b_n\\b_{n-1}\\\vdots\\b_2\\b_1 \end{bmatrix}u(k)\\ \\ y(k) &= \begin{bmatrix} 0 & 0 & \ldots & 0 & 1 \end{bmatrix} x(k) \end{aligned}}_\text{Forma canónica observable}$

Ejercicio

Sea el sistema,

$y(k) + 5y(k-1) + 6y(k-2) = u(k-1) + u(k-2)$

1. Simular el sistema, $y(0) = 2$, $y(1) = -3$, $u(k) = \cos(k)$. Graficar $y(k)$

   $y(k+2) + 5y(k+1) + 6y(k) = u(k+1) + u(k)$ $y(k+2) = - 5y(k+1) - 6y(k) + u(k+1) + u(k)$

    function yk2 = fcn(yk,yk1,k)
    uk1 = cos(k+1);
    uk = cos(k+2);
   
    yk2 = -5*yk1 - 6*yk + uk1 + uk;
   

2. Obtener la forma canónica observable. Graficar $y(k)$ y comparar con el punto 1.

   $\begin{aligned} x(k+1) &= \begin{bmatrix} 0 & -6\\ 1 & -5\\ \end{bmatrix}x(k) + \begin{bmatrix} 1\\1 \end{bmatrix}u(k)\\ y(k) &= \begin{bmatrix} 0 & 1 \end{bmatrix}x(k) \end{aligned}$

   Para $k = 0$:

   $\begin{cases} x_2(0) = y(0) = 2\\ x_2(1) = x_1(0) -5 x_2(0) + u(0) = x_1(0) -10 + 1 = y(1) = -3\\ x_1(0) = 9-3 = 6 \end{cases}$

    function [xk1,yk] = fcn(xk,k)
    A = [0 -6
         1 -5];
    B = [1 1]';
    C = [0 1];
   
    uk = cos(k);
   
    xk1 = A*xk + B*uk;
    yk = C*xk;
   

   Simulando ambos sistemas:

   

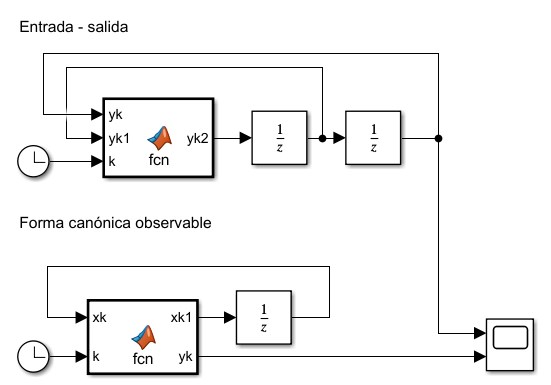
   Se realiza la comparación de las salidas $y(k)$:

   

   $\square$