• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

Introducción a los sistemas en tiempo discreto

De manera general, un sistema en tiempo discreto se define en función del periodo de muestreo $T$ y el instante de muestreo $k$

\[t = kT\]

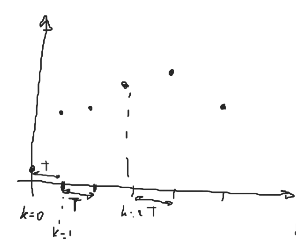
Un sistema en tiempo discreto se representa como,

\[\boxed{x((k+1)T) = f(x(kT),u(kT))}\]

con $T = 1$

\[x((k+1)) = f(x(k),u(k))\]

Para un sistema lineal:

\[(a)\quad\begin{cases} x(k+1) = Ax(k) + Bu(k)\\ y(k) = Cx(k) \end{cases}\]

Su diagrama de bloques es el siguiente:

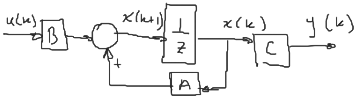
Ejemplos

1. Simular el siguiente sistema en timpo discreto

   \[\begin{cases} x(k+1) = x(k) + 1\\ x(0) = 0 \end{cases}\]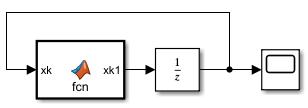

   

    function xk1 = fcn(xk)
    xk1 = xk + 1;
   

   Se configura el solver para tener paso fijo de 1.

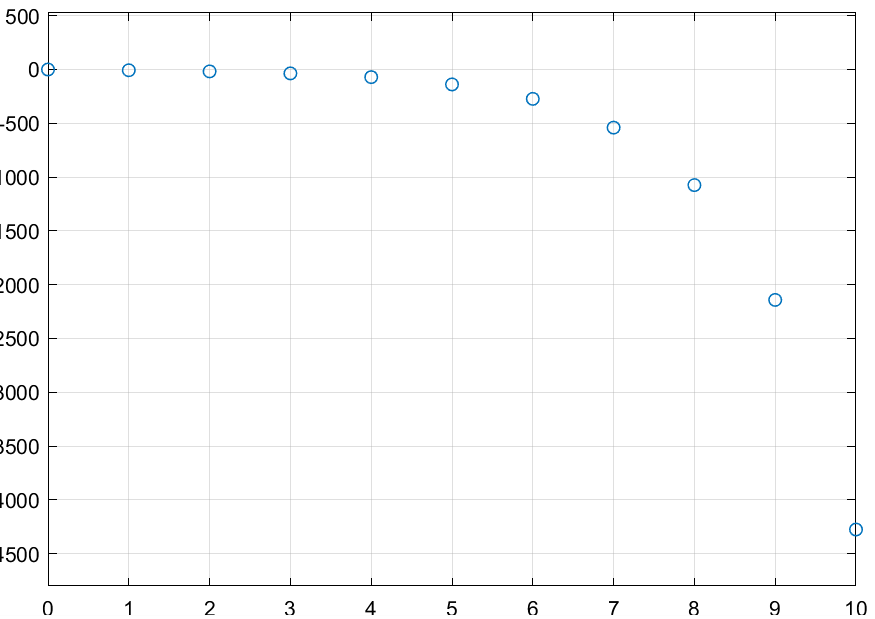
   ##### Resultado

   

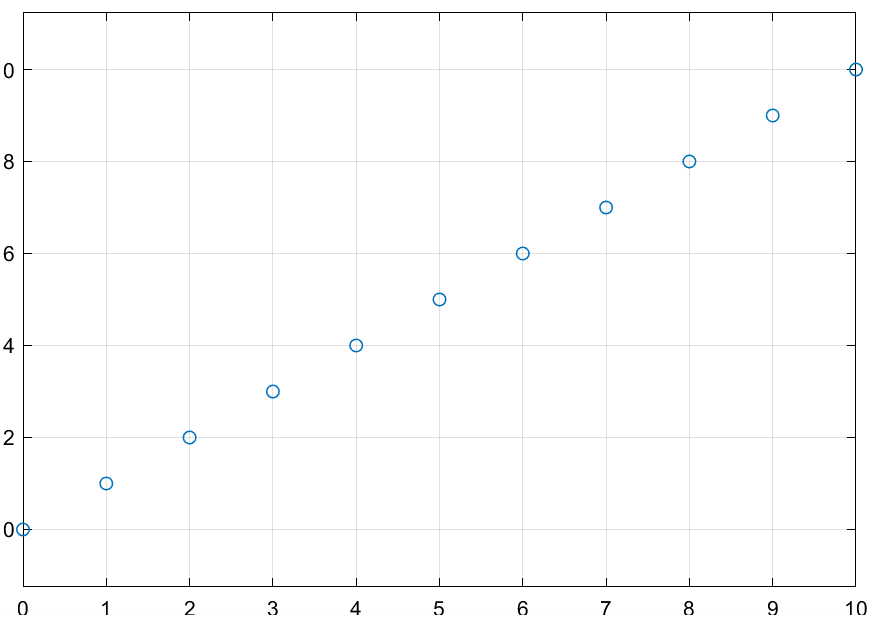
2. Simular el siguiente sistema en timpo discreto

   \[\begin{cases} x_1(k+1) = 2 x_1(k) + 0.5 x_2(k) - 5\\ x_2(k+1) = 0.8 x_2(k) + 2\\ y(k) = x_1(k) - x_2(k)\\ \end{cases}\quad\begin{aligned} x_1(0) &= 2\\ x_2(0) &= -1\\ \end{aligned}\] \[\begin{cases} x(k+1) = \begin{bmatrix} 2 & 0.5\\ 0 & 0.8 \end{bmatrix}x(k) + \begin{bmatrix} -5\\2 \end{bmatrix}u(k)\\ y(k) = \begin{bmatrix} 1 & -1 \end{bmatrix}x(k) \end{cases}\quad,\quad u(k) = 1\]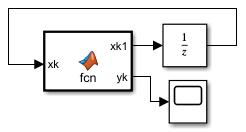

   

    function [xk1,yk] = fcn(xk)
    A = [2 0.5
         0 0.8];
    B = [-5 2]';
    C = [1 -1];
    u = 1;
   
    xk1 = A*xk + B*u;
    yk = C*xk;
   

   Se configura el solver para tener paso fijo de 1.

   ##### Resultado