• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

Modelado de sistemas mecánicos

Considere el sistema masa - resorte

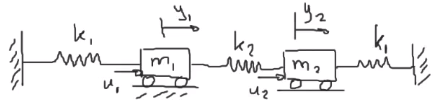
Se asume que no hay fricción entre los bloques y la superficie

1. Obtener la representación entrada - salida.
2. Obtener la representación en espacio de estado.
3. Realizar la simulación del sistema mecánico.

\[k_1 = 10\ N/m\quad,\quad k_2 = 8\ N/m\quad,\quad m_1 = 3kg\quad,\quad m_2 = 1kg\quad\\ u_1 = 10\ N\quad,\quad u_2 = 8\ N\]

Representación entrada - salida

\[\sum F_1 = -k_1 y_1 + u_1 - k_2 (y_1 - y_2) = m_1 \ddot{y_1}\\ \sum F_2 = k_2 (y_1 - y_2) + u_2 - k_1 y_2 = m_2 \ddot{y_2}\\\]

Por lo tanto:

\[\begin{cases} \ddot{y_1} + \dfrac{(k_1 + k_2)}{m_1}y_1 - \dfrac{k_2}{m_1}y_2 = \dfrac{u_1}{m_1}\\ \\ \ddot{y_2} + \dfrac{(k_1 + k_2)}{m_2}y_2 - \dfrac{k_2}{m_2}y_1 = \dfrac{u_2}{m_2} \end{cases}\]

Representación en espacio de estados

Se definen:

\[\begin{cases} x_1 = y_1 & x_3 = y_2\\ x_2 = \dot{y_1} = \dot{x_1} & x_4 = \dot{y_2} = \dot{x_3}\\ \dot{x_2} = \ddot{y_1} & \dot{x_4} = \ddot{y_2}\\ \end{cases}\]

Por lo tanto:

\[\begin{cases} \dot{x_1}= x_2\\ \dot{x_2}= - \dfrac{(k_1 + k_2)}{m_1}x_1 + \dfrac{k_2}{m_1}x_3 + \dfrac{u_1}{m_1}\\ \dot{x_3}= x_4\\ \dot{x_2}= \dfrac{(k_1 + k_2)}{m_2}x_1 - \dfrac{k_2}{m_2}x_3 + \dfrac{u_2}{m_2}\\ \end{cases}\] \[\begin{aligned} \dot{x} &= \begin{bmatrix} 0&1&0&0\\ -\frac{k_1 + k_2}{m_1}&0&\frac{k_2}{m_1}&0\\ 0&0&0&1\\ \frac{k_2}{m_2}&0&-\frac{k_1 + k_2}{m_2}&0\\ \end{bmatrix}x_0 + \begin{bmatrix} 0 & 0\\ \frac{1}{m_1} & 0\\ 0 & 0\\ 0&\frac{1}{m_2}\\ \end{bmatrix}\begin{bmatrix} u_1\\u_2 \end{bmatrix}\\ y &= \begin{bmatrix} 1&0&0&0\\ 0&0&1&0\\ \end{bmatrix}x \end{aligned}\]