Regulación de sistemas lineales
La señal de referencia es una constante.
\[r(t) = r\]El problema consiste en que la salida $y$ se aproxime a la señal de referencia $r$,
\[y(t)\xrightarrow[t\to\infty]{} r\]Considere el sistema SISO:
Caso 1: El sistema $(1)$ tiene un integrador
Se asume que la matriz $A$ tiene un valor propio en $0$ (tiene un integrador).
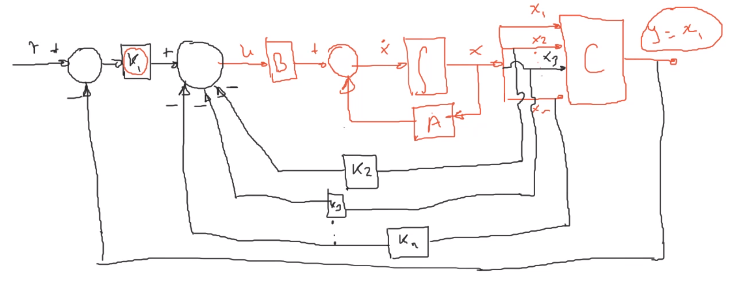
Sustituyendo (2) en (1)
\[\begin{aligned} \dot{x} &= Ax + B(K_1 r - Kx)\\ (3)\quad&= (A - BK) x + B K_1 r\quad\leftarrow{\text{Sistema en lazo cerrado}} \end{aligned}\]Los polos en lazo cerrado se asignarán al sistema $(3)$:
\[p_{lc}(s) = \det(sI - (A-BK)) = (s-\mu_1)(s-\mu_2)\ldots(s-\mu_n)\]En estado estacionario:
\[(4)\quad\lim_{t \to \infty} \dot{x}(t) = (A - BK) \lim_{t\to\infty} x(t) + B K_1 r\]Haciendo $(3) - (4)$:
\[\dot{x} -\lim_{t \to \infty} \dot{x}(t) = (A-BK)\left(x - \lim_{t\to\infty} x(t)\right)\]Se define $e = x - \lim_{t\to\infty} x(t)$, entonces:
\[\boxed{\dot{e}(t) = (A-BK)e(t)}\]Por lo que:
\[e(t) = e^{(A-BK)t}e(0)\]Si $(A - BK)$ es estable (sus valores propios son todos negativos):
\[|e(t)| \xrightarrow[t\to\infty]{}0\]En resumen, el problema de regulación para el caso $(1)$, se resuelve como un problema de ubicación de polos para la matriz $A - BK$
Caso 2: El sistema $(1)$ NO tiene un integrador
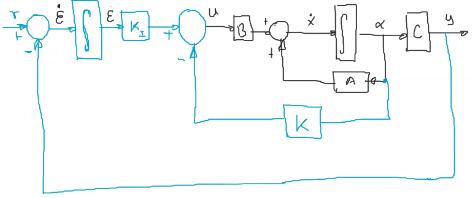
Se utiliza un controlador Proporcional Integral PI:
En el estado estacionario:
\[(4) = \begin{bmatrix} \lim_{t\to\infty} \dot{x}(t)\\ \lim_{t\to\infty} \dot{\varepsilon}(t)\\ \end{bmatrix} = \overbrace{\begin{bmatrix} A & 0\\ -C & 0\\ \end{bmatrix}}^{\bar{A}}\begin{bmatrix} \lim_{t\to\infty} {x}(t)\\ \lim_{t\to\infty} {\varepsilon}(t)\\ \end{bmatrix} + \overbrace{\begin{bmatrix} B\\0 \end{bmatrix}}^{\overline{B}}\lim_{t\to\infty}u(t) + \overbrace{\begin{bmatrix} 0\\1 \end{bmatrix}r}^{r \text{ es cte.}}\]$(3) - (4)$:
\[\begin{aligned} x_c &= x(t) - \lim_{t\to\infty} x(t)\quad,\quad\varepsilon_c = \varepsilon(t) - \lim_{t\to\infty}\varepsilon(t)\\ u_c &= u(t) - \lim_{t\to\infty} u(t) = K_I\varepsilon - Kx - K_I \lim_{t\to\infty} \varepsilon(t) + K \lim_{t\to\infty} x(t) \end{aligned}\] \[\dot{e} = \begin{bmatrix} \dot{x_e}\\ \dot{\varepsilon_e}\\ \end{bmatrix} = \begin{bmatrix} A & 0\\ -C & 0\\ \end{bmatrix}\begin{bmatrix} x_e\\\varepsilon_e \end{bmatrix} + \begin{bmatrix} B\\0 \end{bmatrix}u_e\] \[(5)\quad\dot{e} = \overline{A} e + \overline{B}u_e\] \[u_e = K_I \varepsilon_e - Kx_e = -\begin{bmatrix} K, - K_I \end{bmatrix}e\] \[(6)\quad u_e = -\overbrace{\begin{bmatrix} K,-K_I \end{bmatrix}}^{\overline{K}}e\]Sustituyendo $(6)$ en $(5)$:
\[\dot{e} = \overline{A}e + \overline{B}\begin{bmatrix} -\overline{K}e \end{bmatrix}\] \[\dot{e} = (\overline{A} - \overline{B}\ \overline{K})e\]Por lo tanto, el diseño del controlador PI se resuelve como un problema de ubicación de polos para la matriz $\overline{A} - \overline{B}\ \overline{K}$, donde $\overline{K} = \begin{bmatrix}K,-K_I\end{bmatrix}$.
Selección de polos
El procedimiento para la selección de los polos del sistema $(1)$ a un sistema de segundo orden de la forma:
\[(2)\quad\frac{Y(s)}{U(s)} = \frac{\omega_n^2}{s^2 + 2\xi\omega_ns + \omega_n^2}\]El polinomio característico de la ecuación $(2)$ es:
\[p(s) = s^2 + 2\xi\omega s + \omega_n^2 = 0\]Cuyos polos dominantes son:
\[\boxed{s_{1,2} = -\xi\omega_n \pm \omega_n \sqrt{\xi^2-1}}\]Procedimiento
- Se calculan $\omega_n$ y $\xi$ para que cumplan con los requerimientos del sistema
- Se obtienen los polos determinantes del sistema $s_{1,2}$
- Caso a: Si la planta tiene un cero en $s = q_1$, entonces el valor del polo adicional se asigna igual que $q_1$.
- Caso b: Si la planta NO tiene ceros, el polo adicional se asignará al menos 5 veces más a la izquierda que al parte real de los polos dominantes.
Tips
Para saber si un sistema tiene un integrador:
- La matriz $A$ tiene un valor propio en $0$
- La función de transferencia tiene una s multiplicando en el denominador
Ejercicios
1.
Sea el sistema:
\[\begin{aligned} \dot{x} &= \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ -1 & -5 & -6\\ \end{bmatrix}x + \begin{bmatrix} 0\\1\\1 \end{bmatrix}u\\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}x \end{aligned}\]Determinar las ganancias del controlador tales que los polos del sistema en lazo cerrado se ubiquen en $-2\pm 4j$, $-10$ y $-10$.
\[|r - y| \xrightarrow[t\to\infty]{} 0\]clc; close all; clear all;
% Ejercicio 2
A = [0 1 0
0 0 1
-1 -5 -6];
B = [0 1 1]';
C = [1 0 0];
eig(A) % No tienen integrador
Ab = [A zeros(3,1)
-C 0];
Bb = [B
0];
I = eye(size(Ab,1));
syms s k;
p1 = -2 + 4i; p2 = -2-4i; p3 = -10; p4 = -10;
plc = collect((s-p1)*(s-p2)*(s-p3)*(s-p4))
PLCAb = Ab^4 + 24*Ab^3 + 200*Ab^2 + 800*Ab + 2000*I;
Ckb = [Bb Ab*Bb Ab^2*Bb Ab^3*Bb];
Kb = [0 0 0 1] * Ckb^-1 * PLCAb
eig(Ab - Bb*Kb)
K = Kb(1:end-1)
KI = -Kb(end)
Se obtuvieron los siguientes resultados:
\[\begin{aligned} K &= \begin{bmatrix} 73.3787 & 17.6351 & 0.3649 \end{bmatrix}\\ K_I &= 285.7143 \end{aligned}\]2.
Sea el sistema:
\[\begin{aligned} \dot{x} &= \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & -5 & -6\\ \end{bmatrix}x + \begin{bmatrix} 0\\0\\1 \end{bmatrix}u\\ y &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}x \end{aligned}\]- Diseñar un sistema de regulación, es decir calcular las ganancias del controlador tales que los polos del sistema en lazo cerrado se ubiquen en $-2\pm 2j$ y $-10$.
clc; close all; clear all;
% Ejercicio 2
A = [0 1 0
0 0 1
0 -5 -6];
B = [0 0 1]';
C = [1 0 0];
% Se identifica si tiene integrador
eig(A) % Sí tiene integrador
I = eye(size(A,1));
syms s k;
p1 = -2 + 2i; p2 = -2-2i; p3 = -10;
plc = collect((s-p1)*(s-p2)*(s-p3))
PLCA = A^3 + 14*A^2 + 48*A + 80*I;
Ck = [B A*B A^2*B];
k = [0 0 1] * Ck^-1 * PLCA
eig(A - B*k)
- Realizar la simulación del sistema en lazo cerrado. $r$ escalón unitario.
- Calcular K tal que el máximo sobre impulso sea $12\%$ y el tiempo de establecimiento de $0.5s$
El máximo sobre impulso se calcula como:
\[MP = e^{\frac{\xi\pi}{\sqrt{1-\xi^2}}}\]El tiempo de establecimiento como:
\[T_s = \dfrac{4}{\xi\omega_n}\]Por lo tanto:
\[\begin{cases} \dfrac{4}{\xi\omega_n} = T_s\\ MP = e^{\frac{\xi\pi}{\sqrt{1-\xi^2}}} \end{cases} \begin{cases} \omega_n = \dfrac{4}{T_s\xi}\\ \ln(MP) = \frac{\xi\pi}{\sqrt{1-\xi^2}} \end{cases} \begin{cases} \omega_n = \dfrac{4}{T_s\xi}\\ \xi^2(\ln^2(MP) + \pi^2) = \ln^2(MP) \end{cases}\] \[\begin{cases} \omega_n = \dfrac{4}{T_s\xi}\\ \\ \xi = \sqrt{\dfrac{\ln^2(MP)}{\ln^2(MP) + \pi^2}} \end{cases}\]Por lo tanto para $T_s = 0.5$ y $MP = 0.12$:
\[\begin{cases} \omega_n = 14.3\\ \xi = 0.55 \end{cases}\]Por lo que los polos dominantes son:
\[s_{1,2} = -7.9 \pm 11.95j\]Se verifica si la planta tiene ceros:
sis= ss(A,B,C,0)
tf(sis)
En este caso no tiene ceros, por lo que se procede a definir el $3$er polo como veces la parte real de los polos dominantes.
\[s_3 = 5(-7.9) = -39.5\]Ahora se calcula $K$ para ubicar los polos en $s_1$, $s_2$ y $s_3$.
clc; close all; clear all;
A = [0 1 0
0 0 1
0 -5 -6];
B = [0 0 1]';
C = [1 0 0];
I = eye(size(A,1));
syms s k;
p1 = -7.9 + 11.95i; p2 = -7.9 - 11.95i; p3 = -39.5;
plc = collect((s-p1)*(s-p2)*(s-p3))
PLCA = A^3 + 553/10*A^2 + 13269/16*A + 1296943/160*I;
Ck = [B A*B A^2*B];
k = [0 0 1] * Ck^-1 * PLCA
eig(A - B*k)
Se obtuvo el siguiente resultado:
\[K = \begin{bmatrix} 8105.9 & 824.3 & 49.3 \end{bmatrix}\]