• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

Representación en espacio de estado de sistemas en tiempo discreto

Considere el sistema en timpo discreto:

\[(1)\quad y(k) + a_1 y(k-1) + \ldots + a_n y(k-n) = b_1 u(k-1) + \ldots + b_n u (k-n)\]

donde $y(k)$ es la salida y $u(k)$ es la entrada, $k$ es el instante de muestreo.

Al sistema $(1)$ se le conoce como representación entrada - salida.

Aplicando transformada $\mathcal{Z}$ en ambos lados de $(1)$,

\[\mathcal{Z}\left\{y(k) + a_1 y(k-1) + \ldots + a_n y(k-n)\right\} = \mathcal{Z}\left\{b_1 u(k-1) + \ldots + b_n u (k-n)\right\}\] \[Y(z) + a_1z^{-1}Y(z) + a_2z^{-2}Y(z)+\ldots+a_nz^{-n}Y(z) = b_1z^{-1}U(z) + \ldots + b_nz^{-n}U(z)\] \[\begin{aligned} \frac{Y(z)}{U(z)} &= \frac{b_1z^{-1} + b_2z^{-2} + \ldots + b_nz^{-n}}{1 + a_1z^{-1} + a_2z^{-2} + \ldots + a_nz^{-n}}\frac{z^{n}}{z^{n}}\\ (3)\quad&= \underbrace{\frac{b_1z^{n-1} + b_2z^{n-2} + \ldots + b_n}{z^{n} + a_1z^{n-1} + a_2z^{n-2} + \ldots + a_n}}_\text{Polinomio característico} \end{aligned}\]

El sistema $(1)$ es estable si las raíces del polinomio característico se encuentran dentro del círculo unitario en el plano complejo.

De $(3)$,

\[\frac{Y(z)}{b_1z^{-1} + b_2z^{-2} + \ldots + b_nz^{-n}} = \frac{U(z)}{1 + a_1z^{-1} + a_2z^{-2} + \ldots + a_nz^{-n}} = Q(z)\] \[Q(z) + a_1z^{-1}Q(z) + a_2z^{-2}Q(z) + \ldots + a_nz^{-n}Q(z) = U(z)\] \[(5)\quad\begin{cases} Q(z) = - a_1z^{-1}Q(z) - a_2z^{-2}Q(z) - \ldots - a_nz^{-n}Q(z) + U(z)\\ Y(z) = b_1z^{-1}Q(z) + b_2z^{-2}Q(z) + \ldots + b_nz^{-n}Q(z) \end{cases}\]

A partir de $(5)$ se definen las variables de estado,

\[(6)\quad\begin{cases} X_1(z) = z^{-n}Q(z)\\ X_2(z) = z^{-n+1}Q(z)\\ X_3(z) = z^{-n+2}Q(z)\\ \vdots\\ X_{n-1}(z) = z^{-2}Q(z)\\ X_{n}(z) = z^{-1}Q(z)\\ \end{cases}\]

Multiplicando $(6)$ por $z$,

\[(7)\quad\begin{cases} zX_1(z) = z^{-n+1}Q(z) = X_2(2)\\ zX_2(z) = z^{-n+2}Q(z) = X_3(z)\\ \vdots\\ zX_{n-1}(z) = z^{-1}Q(z) = X_n(z)\\ zX_{n}(z) = Q(z) = -a_1X_n(z) - a_2X_{n-1}(z) - \ldots - a_n x_1(z) + U(z)\\ \\ Y(z) = b_1X_n(z) + b_2X_{n-1}(z) + \ldots + b_n X_1 (z) \end{cases}\]

Aplicando transformada inversa al sistema $(7)$:

\[(8)\quad\begin{cases} x_1(k+1) = x_2(k)\\ x_2(k+1) = x_3(k)\\ \ldots\\ x_{n-1}(k+1) = x_n(k)\\ x_{n}(k+1) = -a_nx_1(k) - a_{n-1}x_2(k) - \ldots - a_2 x_{n-1}(k) + a_1 x_n(k) + u(z)\\ \\ y(k) = b_nx_1(k) + b_{n-1}x_2(k) + \ldots + b_2 x_{n-1} + b_1 x_n (k) \end{cases}\] \[x(k) = \begin{bmatrix} x_1(k)\\ x_2(k)\\ \vdots\\ x_n(k) \end{bmatrix}\] \[\begin{aligned} x(k+1) &= \begin{bmatrix} 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\ 0 & 0 & \ddots & \ddots & 0\\ \vdots & & \ddots & \ddots & \vdots\\ -a_n & -a_{n-1} & \ldots & -a_2 & -a_1\\ \end{bmatrix}x(k) + \left.\begin{bmatrix} 0\\0\\\vdots\\0\\1 \end{bmatrix}u(k)\right\}\text{ Forma canónica controlable}\\ y(k) &= \begin{bmatrix} b_n & b_{n-1} & \ldots & b_2 & b_1 \end{bmatrix}x(k) \end{aligned}\]

Ejercicio

1. Sea el sistema

   \[(2)\quad y(k) + y(k-1) + y(k-2) = u(k-1)\]

   donde, $y(0) = 1$, $y(1) = -2$, $u(k) = \sin(k)$

   1. Simular la ec. $(2)$. Graficar $y(k)$.

      \[\begin{aligned} y(k) &= -y(k-1) - y(k-2) + u(k-1)\\ k = 0\quad\Rightarrow\quad y(0)&= -y(-1) - y(-2) + u(-1)\\ \end{aligned}\]

      dado que no conocemos los valores de $y$ para tiempos negativos:

      \[\rightarrow\quad y(k+2) = -y(k+1) - y(k) + u(k+1)\]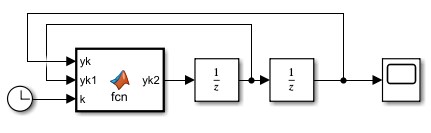

      

       function yk2 = fcn(yk,yk1,k)
       uk1 = sin(k+1);
      
       yk2 = -yk1 - yk + uk1;
      

      En los integradores se ponen las $c.i.$, en la configuración del modelo, se especifica un paso fijo unitario. El resultado es el siguiente:

      

   2. Indicar si el sistema es estable

      \[Y(z) + z^{-1}Y(z) + z^{-2} Y(z) = z^{-1}U(z)\] \[\frac{Y(z)}{U(z)} = \frac{z^{-1}}{1 + z^{-1} + z^{-2}}\frac{z^2}{z^2} = \frac{z}{z^2 + z + 1}\] \[p(z) = z^2 + z + 1 = 0\] \[\Rightarrow \quad z_{1,2} = -\frac{1}{2} \pm \frac{\sqrt{3}}{2} j\] \[|z_1| = 1\quad;\quad|z_2| = 2\]

      Por lo tanto el sistema es estable.

   3. Obtener la forma canónica controlable

      \[\begin{aligned} x(k+1) &= \begin{bmatrix} 0 & 1\\ -1 & -1\\ \end{bmatrix}x(k) + \begin{bmatrix} 0\\1 \end{bmatrix}u(k)\\ y(k) &= \begin{bmatrix} 0 & 1 \end{bmatrix}x(k) \end{aligned}\]

   4. Simular el sistema del punto 3. Graficar $y(k) = Cx(k)$.

      Primero obtenemos las condiciones iniciales:

      Para $k = 0$:
      \(\begin{cases} y(0) = x_2(0) = 1\\ x_1(1) = x_2(0) = 1\\ x_2(1) = - x_1(0) - x_2(0) + u(0) = -2\\ x_1(0) = -x_2(1) - x_2(0) + u(0) = 2 -1 + \sin(0) = 1 \end{cases}\)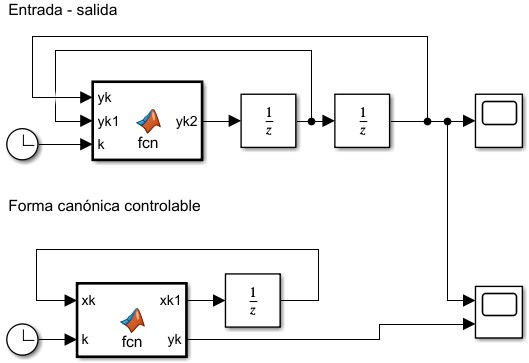

      

       function [xk1,yk] = fcn(xk,k)
       A = [0  1
           -1 -1];
       B = [0 1]';
       C = [0 1];
      
       uk = sin(k);
      
       xk1 = A*xk + B*uk;
       yk = C*xk;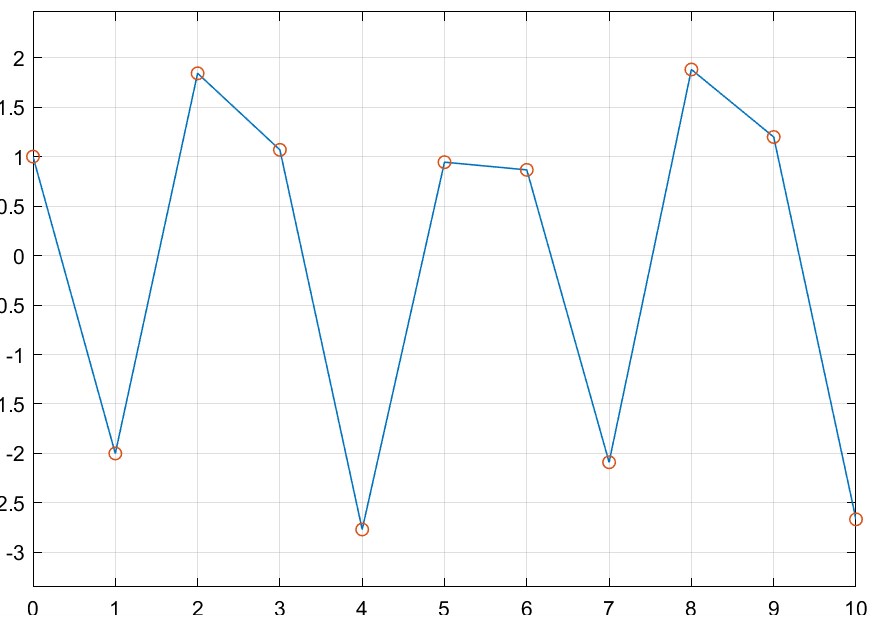
      

      
      \(\square\)

2. Sea el sistema

   \[y(k) + 4y(k-1) + 3y(k-2) = u(k-1)\] \[y(0) = 1\quad,\quad y(1) = 1\quad,\quad u(k) = k\]

   1. Obtener la forma canónica controlable. Graficar y(k)

      \[\begin{cases} \begin{aligned} x(k+1) &= \begin{bmatrix} 0 & 1\\ -3 & -4 \end{bmatrix}x(k) + \begin{bmatrix} 0\\1 \end{bmatrix}u(k)\\ y &= \begin{bmatrix} 0 & 1 \end{bmatrix}x(k) \end{aligned} \end{cases}\]

      Para $k = 0$

      \[\begin{cases} x_2(0) = y(0) = 1\\ x_1(1) = x_2(0) = 1\\ x_2(1) = -3x_1(0) - 4x_2(0) + u(0) = y(1) = 1\\ x_1(0) = \frac{-4x_2(0) + u(0) - x_2(1)}{3} = -1\\ \end{cases}\]

   2. Indicar si el sistema es estable.

      \[Y(z) + 4z^{-1}Y(z) + 3z^{-2} Y(z) = z^{-1}U(z)\] \[\frac{Y(z)}{U(z)} = \frac{z^{-1}}{1 + 4z^{-1} + 3z^{-2}}\frac{z^2}{z^2} = \frac{z}{z^2 + 4z + 3}\] \[p(z) = z^2 + 4z + 3 = 0\] \[\Rightarrow\quad\begin{aligned} z_{1} &= -1\\ z_{2} &= -3\\ \end{aligned}\]

      Por lo tanto el sistema no es estable.

   3. Simular el sistema $(1)$. Graficar $y(k)$. Comparar con la gráfica del punto 1.

      \[y(k+2) + 4y(k+1) + 3y(k) = u(k+1)\] \[y(k+2) = -4y(k+1) - 3y(k) + u(k+1)\]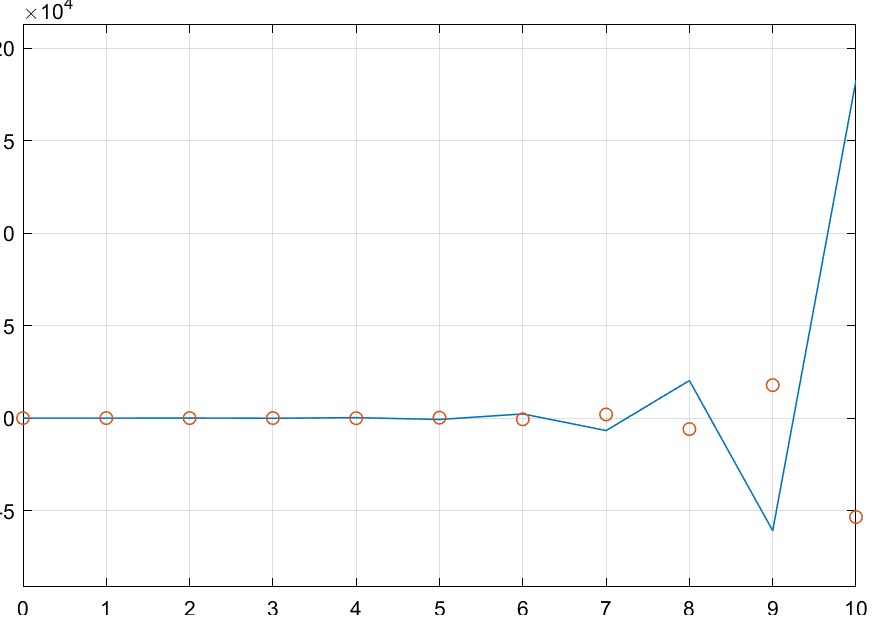

      

   \[\square\]