Retroalimentación basada en observadores de estado

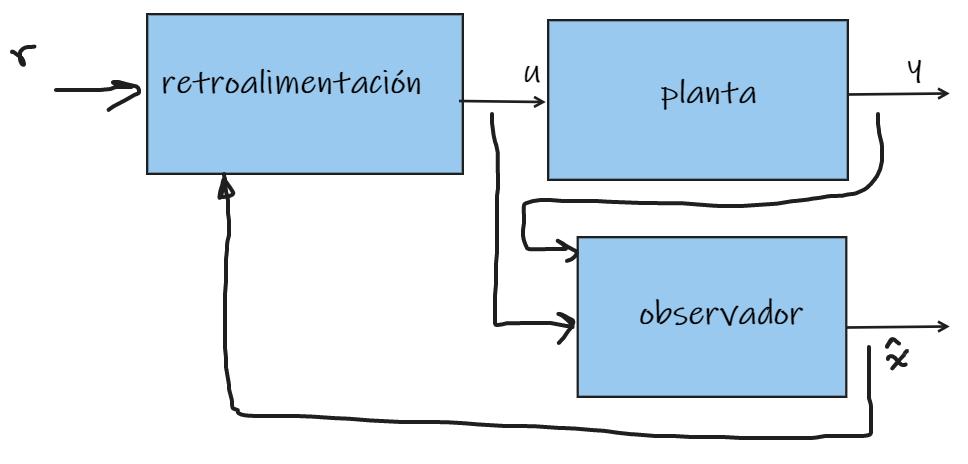
Diagrama de bloques de retroalimentación por observadores de estado

Demostrar que el sistema interconectado es estable.

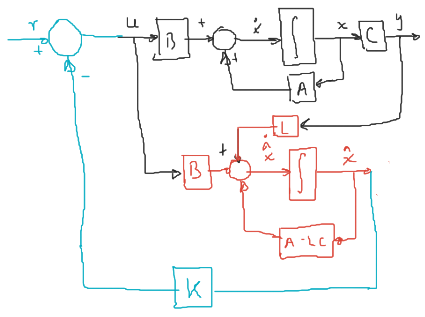
Diagrama de control

\[\begin{aligned} (1)\quad \dot{x} &= Ax + Bu\quad,\quad y = Cx\\ (2)\quad \dot{\hat{x}} &= (A - LC)\hat{x} + Bu + Ly\\ (3)\quad u &= r-k\hat{x}\\ \end{aligned}\]

Sustituyendo $(3)$ en $(1)$:

\[\begin{aligned} \dot{x} &= Ax + B(r-k\hat{x})\\ (4)\quad \dot{x} &= Ax -Bk\hat{x} + Br\\ \end{aligned}\]

Sustituyendo $(3)$ en $(2)$:

\[\begin{aligned} \dot{\hat{x}} &= (A - LC)\hat{x} + B(r-k\hat{x}) + LCx\\ (5)\quad \dot{\hat{x}} &= LCx + (A - LC - Bk)\hat{x} + Br\\ \end{aligned}\]

De las ecuaciones $(4)$ y $(5)$

\[\dot{\mathcal{X}} = \begin{bmatrix} \dot{x}\\\dot{\hat{x}} \end{bmatrix} = \underbrace{\begin{bmatrix} A & -Bk\\ LC & A-LC-Bk\\ \end{bmatrix}}_\mathcal{A}\underbrace{\begin{bmatrix} x\\\hat{x} \end{bmatrix}}_\mathcal{X} + \underbrace{\begin{bmatrix} B\\B \end{bmatrix}}_\mathcal{B}T\]

Sea la transformación $X = T\tilde{X}$, con $T$ invertible

\[\begin{aligned} T\tilde{\dot{\tilde{\mathcal{X}}}} &= \mathcal{A}T\mathcal{\tilde{X}}+ \mathcal{B}r\\ \tilde{\dot{\tilde{\mathcal{X}}}} &= T^{-1}\mathcal{A}T{\tilde{\mathcal{X}}}+ T^{-1}\mathcal{B}r\\ \end{aligned}\]

Se propone:

\[T = \begin{bmatrix} I & 0 \\ I & I \\ \end{bmatrix}\quad;\quad T^{-1} = \begin{bmatrix} I & 0 \\ -I & I \\ \end{bmatrix}\]

Por lo tanto:

\[\begin{aligned} T^{-1}{A}T &= \begin{bmatrix} I & 0\\ -I & I\\ \end{bmatrix}\begin{bmatrix} {A} & -{B}k\\ LC & {A}-LC-{B}k\\ \end{bmatrix}\begin{bmatrix} I & 0\\ I & I\\ \end{bmatrix}\\ &= \begin{bmatrix} {A} & -{B}k\\ -{A}+LC & {B}k + {A}-LC-{B}k \end{bmatrix}\begin{bmatrix} I & 0\\ I & I\\ \end{bmatrix}\\ &= \begin{bmatrix} {A} - {B}k & -{B}k\\ -{A}+LC+{A}-LC & A - LC\\ \end{bmatrix} = \begin{bmatrix} {A}-{B}k & -{B}k\\ 0 & {A}-LC\\ \end{bmatrix}\\ \end{aligned}\]

Las matrices

\[\begin{bmatrix} {A} & -{B}k\\ LC & {A}-LC-{B}k\\ \end{bmatrix}\quad\text{y}\quad \begin{bmatrix} {A}-{B}k & -{B}k\\ 0 & {A}-LC\\ \end{bmatrix}\]

Es decir, $\mathcal{A}$ y $T^{-1}\mathcal{A}T$ son similares:

\[\lambda(\mathcal{A}) = \underbrace{\lambda({A} - {B}k)}_{\text{polos por retroalimentación}} \cup \overbrace{\lambda(A-LC)}^\text{Polos del observador}\]

El diseño de un observador de estado y el diseño de un controlador se pueden hacer de manera independiente, a esto se le conoce como Principio de separación.