• Notas
• 7mo Semestre
• Control de Sistemas Mecatrónicos

Ubicación de polos

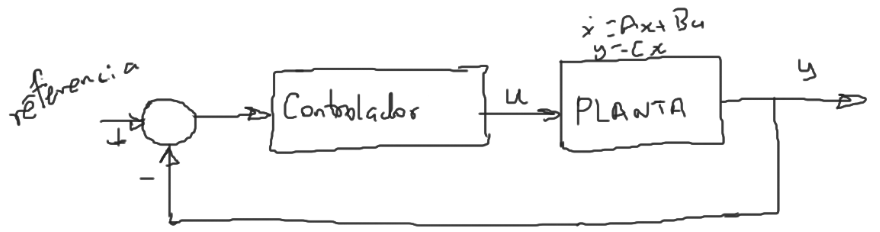
Donde:
$y$ es la salida disponible
$u$ es la señal de control

Si la señal de referencia es una constante

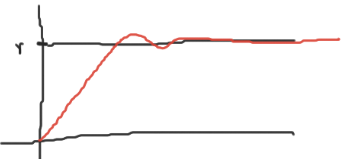
Si la señal de referencia varía con respecto al tiempo

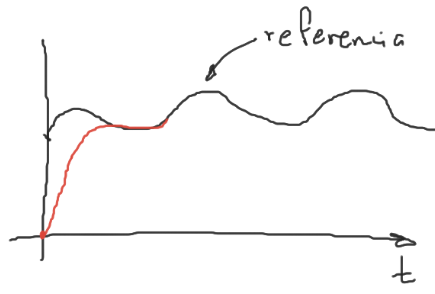
Ubicación de polos por retroalimentación de estado

Considere el sistema SISO

\[(1)\begin{cases} \dot{x} &= Ax + Bu\\ y &= Cx \end{cases}\]

• Se asume que el sistema $(1)$ es controlable
• Se asume que se conoce todo el vector de estado $x$

El polinomio característico del sistema $(1)$ es,

\[\begin{aligned} p(s) &= \det(sI-A) = s^n + a_1 s^{n-1}+ a_2 s^{n-2} + \cdots + a_{n-1} s + a_n\\ &=(s-q_1)(s-q_2)\cdots(s-q_n) \end{aligned}\]

Donde: $q_1, q_2, \ldots, q_n$ son los polos en lazo abierto.

El problema de ubicación de polos consiste en asignar vectores $\mu_1, \mu_2,\ldots,\mu_n$ al polinomio característico en lazo cerrado.

\[\begin{matrix}q_1\\ q_2\\ \vdots\\ q_n\end{matrix} \longrightarrow \begin{matrix}\mu_1\\ \mu_2\\ \vdots\\ \mu_n\end{matrix}\]

Se define la retroalimentación de estado:

\[\begin{aligned} (2)\quad u &= r-kx\quad,\quad k=[k_1\ k_2\ \ldots\ k_n]:1\times n\\ &= r-[k_1\ k_2\ \ldots\ k_n]\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\\ &= r-(k_1x_1+k_2x_2+\ldots+k_nx_n) \end{aligned}\] \[u = r - \sum^n_{i=1}k_ix_i\]

Sustituyendo $(2)$ en $(1)$:

\[\begin{aligned} \dot{x} &= Ax + B(r-kx)\\ &= Ax + Br-Bkx\\ \end{aligned}\] \[(3)\quad \dot{x} = (A-Bk)x + Br\quad\text{Sistema en lazo cerrado}\]

Calculando el polinomio característico:

\[\begin{aligned} p_{LC}(s) &= \det(sI-(A-Bk)) = s^n + \tilde{a}_1 s^{n-1}+ \tilde{a}_2 s^{n-2} + \cdots + \tilde{a}_{n-1} s + \tilde{a}_n\\ &=(s-\mu_1)(s-\mu_2)\cdots(s-\mu_n) \end{aligned}\]

Procedimiento

1. Calcular el polinomio característico en función de los polos deseados en lazo cerrado.

\[p_{LC}=(s-\mu_1)(s-\mu_2)\cdots(s-\mu_n) = s^n + \tilde{a}_1 s^{n-1}+ \cdots + \tilde{a}_n\]

1. Calcular $p_{LC}$ en términos de la ganancia $k$

\[p_{LC}(s) = \det(sI-(A-Bk)) = s^n + \tilde{a}_1 s^{n-1}+ \tilde{a}_2 s^{n-2} + \cdots + \tilde{a}_{n-1} s + \tilde{a}_n\\\]

1. Igualar los coeficientes

\[\tilde{a}_1(k) = a_1\quad,\quad \tilde{a}_2(k) = a_2\quad,\quad \ldots\quad,\quad \tilde{a}_n(k) = a_n\]

1. Realizar la comprobación. Calcular los valores propios de $(A-Bk)$

Ubicación de polos por forma canónica controlable

Se define la retroalimentación de estado:

\[u = r-kx = r - kP^{-1}\tilde{x} = r - \bar{k}\tilde{x}\] \[\tilde{x} = Px\\ x = P^{-1}\tilde x\\ \bar{k} = kP^{-1} \Rightarrow k=\bar{k}P\]

Sustituyendo $\tilde x = Px$ en (1)

\[P^{-1}\dot{\tilde x} = AP^{-1}\tilde x + Bu\\ \begin{aligned} \dot{\tilde x} &= PAP^{-1}\tilde x + PBu\\ &= PAP^{-1}\tilde x + PB(r-kP^{-1}\tilde x)\\ &= PAP^{-1}\tilde x + PBr-PBkP^{-1}\tilde x\\ &= P(A-Bk)P^{-1}\tilde x + PBr \end{aligned}\]

Por lo que los sistemas $(3)$ y $(4)$ son similares.

Es decir, $A-Bk$ y $P(A-Bk)P^{-1}$ tienen los mismos valores propios

\[\begin{aligned} p_{LC} &= det(sI-(A-Bk)) = det(sI - P(A-Bk)P^{-1})\\ &= s^n + \tilde{a}_1 s^{n-1}+ \tilde{a}_2 s^{n-2} + \cdots + \tilde{a}_{n-1} s + \tilde{a}_n\\ \end{aligned}\] \[\begin{aligned} \tilde{A}-\tilde{B}\bar{k}= \begin{bmatrix} -\tilde{a_1} &-\tilde{a_2} &-\tilde{a_3} & \cdots & -\tilde{a_n}\\ 1&0&\cdots&\cdots&0\\ 0&1&0&\cdots&\vdots\\ \vdots&\ddots&\ddots&\ddots\\ 0&\cdots&\cdots&1&0\\ \end{bmatrix} &= \begin{bmatrix} -a_1 &-a_2 &-a_3 & \cdots & -a_n\\ 1&0&\cdots&\cdots&0\\ 0&1&0&\cdots&\vdots\\ \vdots&\ddots&\ddots&\ddots\\ 0&\cdots&\cdots&1&0\\ \end{bmatrix} - \begin{bmatrix}1\\0\\\vdots\\0\end{bmatrix}[\bar{k}_1\ \bar{k}_2\ \ldots \bar{k}_n]\\ &=\begin{bmatrix} -a_1-\bar{k}_1 &-a_2-\bar{k}_2 &-a_3-\bar{k}_3 & \cdots & -a_n-\bar{k}_n\\ 1&0&\cdots&\cdots&0\\ 0&1&0&\cdots&\vdots\\ \vdots&\ddots&\ddots&\ddots\\ 0&\cdots&\cdots&1&0\\ \end{bmatrix} \end{aligned}\]

Por lo tanto:

\[\begin{matrix} -\tilde{a}_1 = -a_1 - \bar{k}_1\\ -\tilde{a}_2 = -a_2 - \bar{k}_2\\ \vdots\\ -\tilde{a}_n = -a_n - \bar{k}_n\\ \end{matrix}\quad\Longrightarrow\quad\begin{matrix} \bar{k}_1 = \tilde{a}_1 - a_1\\ \bar{k}_2 = \tilde{a}_2 - a_2\\ \vdots\\ \bar{k}_n = \tilde{a}_n - a_n\\ \end{matrix}\]

Procedimiento

1. Polinomio característico en lazo abierto. Determinar $a_1, a_2, \ldots, a_n$
2. Calcular $P^{-1}$, luego $P = (P^{-1})^{-1}$
3. Polinomio característico en lazo cerrado $\tilde{a}_1, \tilde{a}_2, \ldots, \tilde{a}_n$
4. Calcular $\bar{k} = [\tilde{a}_1-a_1,\tilde{a}_2-a_2, \ldots, \tilde{a}_n-a_n]$
5. Obtener $k = \bar k P$
6. Comprobación

   >> eig(A-Bk)
   

\[\mu_1\\ \mu_2\\ \vdots\\ \mu_n\\\]

Teorema de Cayley-Hamilton

Toda matriz satisface su polinomio característico.

\[\begin{aligned} p(s) &= \det(sI-A) = s^n + a_1 s^{n-1}+ a_2 s^{n-2} + \cdots + a_{n-1} s + a_n\\ &= A^n + a_1 A^{n-1} + a_2 A^{n-2} + \cdots + a_n I = 0\\ \end{aligned}\]

Ubicación de polos por el método de Ackerman

Es un método muy importante y de hecho matlab tiene un comando para esto:

Se tiene el sistema SISO

\[(1)\begin{cases} \dot{x} &= Ax + Bu\\ y &= Cx \end{cases}\]

• Se asume que el sistema $(1)$ es controlable
• Se asume que se conoce todo el vector de estado $x$

El polinomio característico del sistema $(1)$ es,

\[\begin{aligned} p(s) &= \det(sI-A) = s^n + a_1 s^{n-1}+ a_2 s^{n-2} + \cdots + a_{n-1} s + a_n\\ &=(s-q_1)(s-q_2)\cdots(s-q_n) \end{aligned}\]

Donde: $q_1, q_2, \ldots, q_n$ son los polos en lazo abierto.

Si $u = r-kx$

\[\dot{x} = (A-Bk)x + Br\qquad\leftarrow \text{Sistema en lazo cerrado}\]

Cuyo polinomio característico (lazo cerrado):

\[\begin{aligned} p_{LC}(s) &= \det(sI-(A-Bk)) = s^n + \tilde{a}_1 s^{n-1}+ \tilde{a}_2 s^{n-2} + \cdots + \tilde{a}_{n-1} s + \tilde{a}_n\\ &=(s-\mu_1)(s-\mu_2)\cdots(s-\mu_n) \end{aligned}\]

Por lo tanto:

\[P_{LC}(A-Bk)= (A-Bk)^n + \tilde{a}_1 (A-Bk)^{n-1} + \tilde{a}_2 (A-Bk)^{n-2} + \cdots + \tilde{a}_n I = 0\\\]

Considerando $n = 3$

\[\begin{aligned} p_{LC}(s) &= s^3 + \tilde{a}_1 s^{2}+ \tilde{a}_2 s +\tilde{a}_3\\ P_{LC}(A-Bk)&= (A-Bk)^3 + \tilde{a}_1 (A-Bk)^{2} + \tilde{a}_2 (A-Bk)^{n-2} + \cdots + \tilde{a}_n I = 0\\ \end{aligned}\] \[(A-Bk)^2 = A^2 - ABk - BkA + (Bk)^2 = A^2 - ABk - Bk(A-Bk)\] \[(A-Bk)^3 = (A-Bk)(A-Bk)^2 = A^3 - A^2Bk - ABk(A-Bk) - Bk(A-Bk)^2\]

Por lo tanto:

\[A^3 - A^2Bk - ABk(A-Bk) - Bk(A-Bk)^2 + \tilde{a}_1A^2 - \tilde{a}_1ABk - \tilde{a}_1Bk(A-Bk) + \tilde{a}_2A - \tilde{a}_2Bk + \tilde{a}_3I = 0\] \[\underbrace{A^3 + \tilde{a}_1A^2 + \tilde{a}_2A + \tilde{a}_3I}_{p_LC(A)\neq0} - \underbrace{[B\ AB\ A^2B]}_{C}\begin{bmatrix} k(A-Bk)^2 + \tilde{a}_1k(A-Bk) + \tilde{a}_2k\\ k(A-Bk) + \tilde{a}_1k\\ k \end{bmatrix} = 0\] \[P_{LC}(A) = C\begin{bmatrix} k(A-Bk)^2 + \tilde{a}_1k(A-Bk) + \tilde{a}_2k\\ k(A-Bk) + \tilde{a}_1k\\ k \end{bmatrix}\] \[C^{-1}P_{LC}(A) = \begin{bmatrix} k(A-Bk)^2 + \tilde{a}_1k(A-Bk) + \tilde{a}_2k\\ k(A-Bk) + \tilde{a}_1k\\ k \end{bmatrix}\]

Finalmente:

\[\boxed{[0\ 0\ \ldots\ 0\ 1]C^{-1}P_{LC}(A)}\\ \text{Fórmula de Ackerman}\]

Ecuación de Lyapunov

Sea una matriz $F : n\times n$ con valores propios iguales que los polos deseados en lazo cerrado, entonces

\[A - Bk = TFT^{-1}\qquad ,T:n\times n \text{ es invertible}\]

Se construye $F$ para que tenga los mismos valores propios de $(A-Bk)$, como una matriz diagonal por bloques para que sea más fácil. Con bloques de Jordan para valores repetidos deseados (en la diagonal con 0s abajo y 1s arriba).

Ejemplo

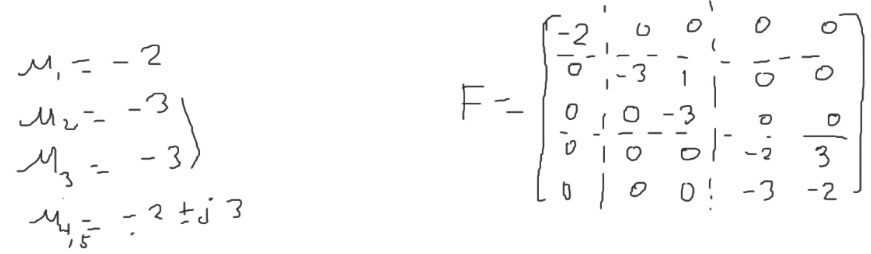
Despejando

\[AT - BkT = TF\\ AT - TF - B\underbrace{kT}_{\bar{k}} = 0\\\] \[\boxed{AT - TF - B\bar{k} = 0}\\ \text{Ecuación de Lyapunov}\]

Procedimiento

1. Construir una matriz $F$ con los polos deseados en lazo cerrado. Se recomienda que sea una matriz diagonal por bloques.
2. Proponer $\bar{k}$ tal que el par $(F,\bar{k})$ sea observable.
3. Resolver la ecuación de Lyapunov para encontrar $T$.

\[T = \text{lyap}(A,-F,-B\bar{k})\]

1. $k = \bar{k}T^{-1}$