Esfuerzo de impacto

Un bloque D con masa $m = 80\ kg$ se deja caer de una altura desde el reposo, la altura $h = 40\ mm$ antes de impactar el punto C; que es el punto medio de una viga simplemente apoyada AB (de aluminio). La sección transversal de la viga es rectangular de base $40\ mm$ y altura $20\ mm$, $L = 1\ m$, $E=70\ GPa$, determine:
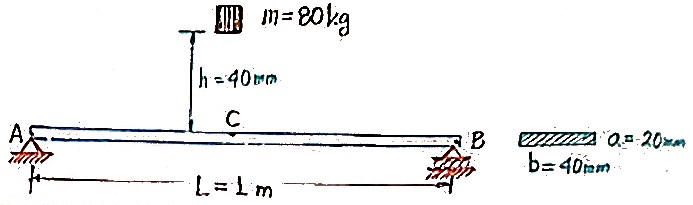
1. La deflexión máxima del punto $C$ de la viga.
2. El esfuerzo máximo que ocurre en la viga.
## Principio de trabajo y energía
Posición $I$: Debido a que el cuerpo D se deja caer del reposo, la energía cinética del cuerpo y la energía de deformación de la viga son cero.
Posición $II$: La energía de deformación de la viga es máxima y la energía cinética del cuerpo D es cero.

\[\begin{aligned} EI_zy'' &= M<x>\\ &= \frac{F}{2}<x> - F<x - \frac{L}{2}>\\ EI_zy'&= \frac{F}{4}<x>^2 - \frac{F}{2}<x - \frac{L}{2}>^2 + C_1\\ EI_zy&= \frac{F}{12}<x>^3 - \frac{F}{6}<x - \frac{L}{2}>^3 + C_1<x> + C_2\\ \end{aligned}\] \[y(0) = 0\quad\Rightarrow\quad \boxed{C_2 = 0}\] \[\begin{aligned} y(L) = 0 &= \frac{FL^3}{12} - \frac{F}{6}\left(\frac{L}{2}\right)^3 + C_1L\\ &= \frac{FL^3}{12} - \frac{FL^3}{48} + C_1L\\ \end{aligned}\] \[C_1 = \frac{FL^2 - 4FL^2}{48} = \frac{-3FL^2}{48}\]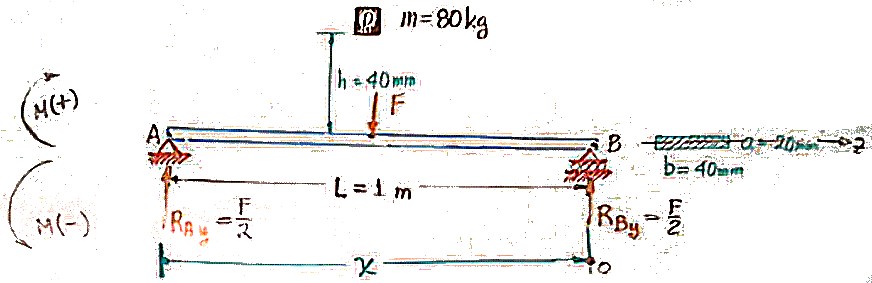
Sustituyendo $C_1$ y $C_2$:
\[EI_zy = \frac{F}{12}<x>^3 - \frac{F}{6}<x - \frac{L}{2}>^3 - \frac{3FL^2}{48}<x>\] \[y\left(\frac{L}{2}\right) = y_{max}\] \[EI_zy_{max} = \frac{FL^3}{96} - \frac{3FL^3}{96} = -\frac{FL^3}{48}\]
Por lo tanto:
\[y_{max} = -\frac{F_{max}L^3}{48EI_z}\]
### Energía de deformación
Es el área bajo la curva en el diagrama fuerza - deformación:
\[U = \frac{1}{2}Fy\]
Por lo tanto se calcula la energía de deformación máxima:
\[U_{max} = \frac{1}{2}F_{max}y_{max} = \underbrace{\frac{24EI_z}{L^3}y_{max}^2}_\text{E. de deformación de viga}\]
La masa D desarrolla un trabajo para recorrer la altura $h$ y deformar la viga ($y_{max}$).
\[W = mg(h + y_{max})\]
Igualando las energías:
\[\frac{24EI_z}{L^3}y_{max}^2 = mg(h + y_{max})\] \[\frac{24EI_z}{L^3}y_{max}^2 - mgy_{max} - mgh = 0\] \[\frac{24(70\times10^{9})\frac{1}{12}(0.04)(0.02)^3}{1}y_{max}^2 - (80)(9.81)y_{max} - (80)(9.81)(0.04) = 0\]
Solucionando:
\[\begin{aligned} y_{max1} &= 36.6\ mm\quad\checkmark\\ y_{max2} &= -19\ mm\quad\times \end{aligned}\]
Por lo tanto:
\[\boxed{y_{max} = 36.6\ mm}\]
Para calcular el esfuerzo por impacto:
\[\sigma_{flex} = \frac{V_{max}C}{I_z} = \frac{\frac{F_{max}L}{4}C}{I_z}\] \[F_{max} = \frac{48EI_z}{L^3} = 3225.6\ N\]
Por lo tanto:
\[\sigma_{flex} = \frac{(3225.6)(1)(\frac{1}{4})(0.01)}{\frac{1}{2}(0.04)(0.02)^3} = 302.4\times10^6\ Pa\] \[\boxed{\sigma_{flex} = 302.4\ MPa}\]
El factor de seguridad es:
\[N = \frac{S_{yp}}{\sigma_{flex}} = \frac{276}{302.4} = 0.91 < 1\quad\times\]
Por lo que es deformación plástica.

Si no hubiera impacto:
\[\sigma_{flex} = \frac{(80)(9.81)(\frac{1}{4})(0.01)}{\frac{1}{12}(0.04)(0.02)^3} = 73.5\ MPa\]
Por lo que
\[N = \frac{276}{73.5} = 3.75\quad>>\quad1\]