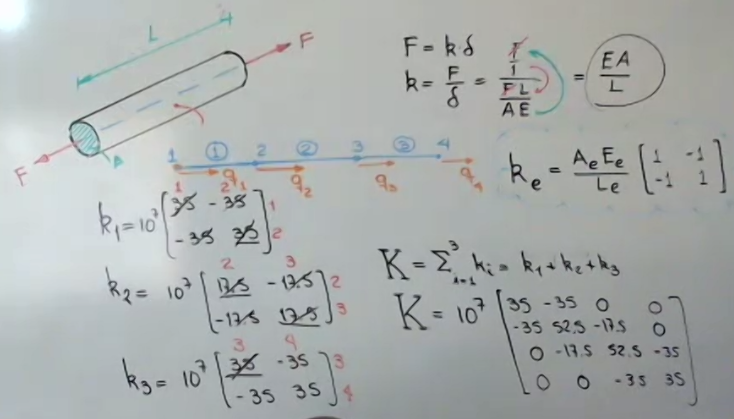Introducción
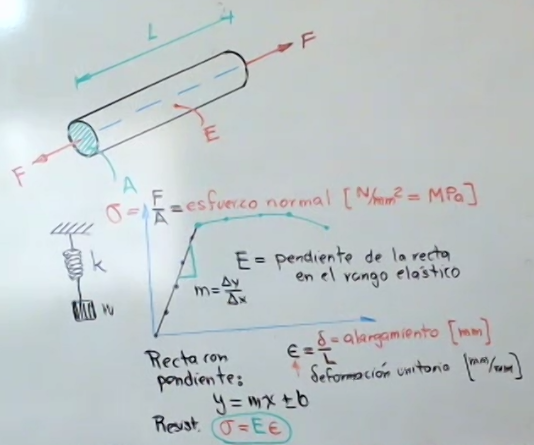
Resistencia
\[\sigma = E\epsilon\] \[\epsilon = \dfrac{\delta}{L}\]Rigidez
\[\delta = \dfrac{FL}{AE} = \dfrac{\sigma L}{E}\]Debido a las propiedades elásticas de los sólidos, estos se pueden representar como un resorte.
\[F = k\delta\] \[k = \dfrac{F}{\delta} = \dfrac{F}{\dfrac{FL}{AE}} = \dfrac{AE}{L}\]En forma matricial:
\[F = KQ\]Donde:
$K$ es la matriz ensamblada de rigidez y sus dimensiones dependen de los grados de libertad del sistema.
$Q$ Es el vector de fuerzas aplicadas en los nodos del sistema.
Suma en ensamble de constantes de rigidez
Ejercicio
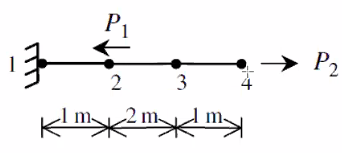
Considere la estructura compuesta de tres elementos lineales llamados barras como se muestra en la figura de abajo. el material de los dos elementos es: $E=70GPa$, $A=0.005m^2$ $P_1 = 10kN$, $P_2 = 15kN$. En un momento determinado en la operación del elemento máquina, Determine:
- La matriz de rigidez global.
- Los desplazamientos de los nodos 2, 3, y 4.
- La reacción en el apoyo en el nodo 1.
- El esfuerzo axial en cada barra.