Aprendizaje Hebbiano
Postulado de Hebb
“Cuando el axón de una célula A, está suficientemente cerca como para estimular a una célula B y repetida o persistentemente está involucrada en su proceso de disparo, algún tipo de crecimiento o de cambio metabólico toma lugar en una o ambas células de tal forma que, la eficiencia de A, como una de las células responsables de disparar a B, se ve incrementada.”
Esto quiere decir que la neurona aprende, con respecto a las entradas que tiene y modifica su comportamiento conforme más repetitivo sean las entradas.
Regla de Hebb
Esta regla es el modelo matemático del postulado antes presentado:
\[\boxed{\omega_i^{new} = \omega_i^{old} + \alpha x_i y_i}\] \[\alpha > 0\quad;\quad \forall i = 0,1,\ldots,n\]Donde $\alpha$ es la razón de aprendizaje. De este valor depende si la neurona converge o diverge al ser entrenada.
Tomando la neurona bipolar como unidad lógica funcional; que utiliza la función signo como función de activación:
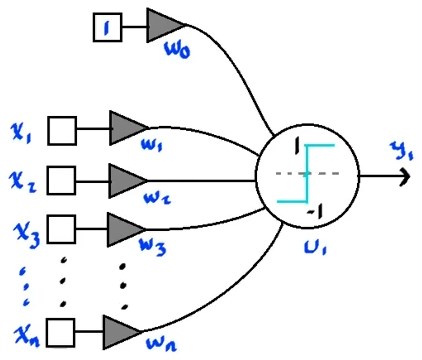
Esta neurona sólo acepta los valores $\left{-1,1\right}$ como valores para sus entradas.
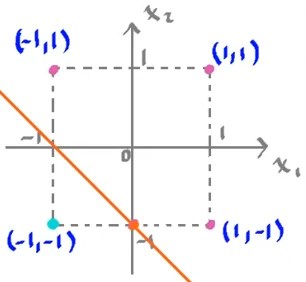
Si se quisiera entrenar esta neurona para seguir el comportamiento de la función OR bipolar, siguiendo la regla de Hebb, se seguirían los siguientes pasos:
OR bipolar
| $x_1$ | $x_2$ | $y$ |
| - | - | - |
| $-1$ | $-1$ | $-1$ |
| $-1$ | $1$ | $1$ |
| $1$ | $-1$ | $1$ |
| $1$ | $1$ | $1$ |
Iniciando los valores en de $\omega$ en $0$, con un valore de $\alpha = 1$:
\[\begin{aligned} &\begin{cases} \omega_0^{new} = 0 + (1) (-1) = -1\\ \omega_1^{new} = 0 + (-1) (-1) = 1\\ \omega_2^{new} = 0 + (-1) (-1) = 1\\ \end{cases}\quad\begin{cases} \omega_0^{new} = -1 + (1) (1) = 0\\ \omega_1^{new} = 1 + (-1) (1) = 0\\ \omega_2^{new} = 1 + (1) (1) = 2\\ \end{cases}\\ \\ &\begin{cases} \omega_0^{new} = 0 + (1) (1) = 1\\ \omega_1^{new} = 0 + (1) (1) = 1\\ \omega_2^{new} = 2 + (-1) (1) = 1\\ \end{cases}\quad\begin{cases} \omega_0^{new} = 1 + (1) (1) = 2\\ \omega_1^{new} = 1 + (1) (1) = 2\\ \omega_2^{new} = 1 + (-1) (1) = 2\\ \end{cases}\\ \end{aligned}\]Estos valores se pueden comprobar, graficando la frontera de desición en el espacio de entrdas:
\[\begin{aligned} x_2 &= -\frac{\omega_1}{\omega_2}x_1 - \frac{\omega_0}{\omega_2}\\ &= -\frac{2}{2}x_1 - \frac{2}{2}\\ &= -x_1 - 1\\ \end{aligned}\]