• Notas
• 7mo Semestre
• Sistemas Neurodifusos
• Redes Neuronales

Neurona artificial

La neurona biológica

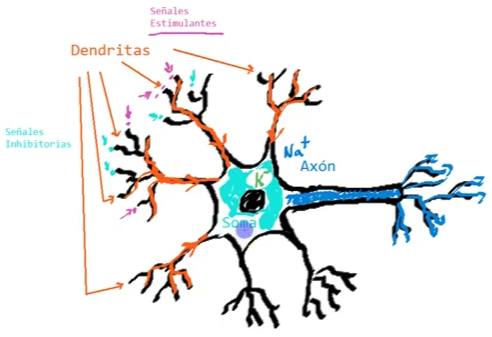
Se compone de las siguientes partes:

• Cuerpo (soma): Contiene el núcleo de la neurona.
• Dendritas: Ramificaciones donde se reciben las señales de entrada, de otras neuronas u órganos.
• Axón: Incrementa y propaga el potencial de activación de la neurona, que se termina conectando con otras neuronas.

Las neuronas del cerebro humano, están conectadas con miles de neuronas a la entrada y a la salida.

Las neuronas pueden recibir señales de tipo estimulantes e inhibitorias, que al ser evaluadas, se determina si la neurona se activa o no.

El cerebro contiene muchas neuronas conectadas, se estima que al rededor de $10^{15}$. Estas se comunican por el proceso llamado sinapsis. Además, dichas conexiones no son fijas, si no que se pueden reconfigurar.

La neurona artificial

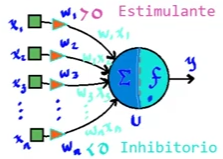
Donde:
$x_i$: Unidades de entrada
$w_i$: Pesos sinápticos
$\Sigma$: Concentración de la información de entrada
$a$: Valor de activación o valor de entrada

\[a = \Sigma^n_{i=1} w_i x_i\quad:\quad\text{Suma ponderada de las entradas}\]

$f$: Función de activación o función de transferencia
$y$: Salida de la neurona

\[y = f(a - \phi)\]

Función de activación

La función de activación define el comportamiento de una neurona frente a las entradas, entre las funciones de activación más comúnes están:

Escalón unitario

\[f(a-\phi) = \begin{cases} 1 & a \geq \phi\\ 0 & a < \phi\\ \end{cases}\]

Signo

\[f(a - \phi) = \begin{cases} 1 & a \geq \phi\\ -1 & a < \phi \end{cases}\]

Lineal

\[f(a - \phi) = a -\phi\]

Sigmoide

\[f(a - \phi) = \frac{1}{1+e^{\phi-a}}\]

Gaussiana

\[f(a - \phi) = \frac{1}{1+e^{\phi-a}}\]

Comportamiento con diferentes pesos sinápticos

El comportamiento de una neurona depende de los pesos sinápticos, por ejemplo considerando una neurona con una función de activación escalón unitario.

\[f(a-\phi) = \begin{cases} 1 & a \geq \phi\\ 0 & a < \phi\\ \end{cases}\]

Los pesos sinápticos se pueden adaptar para que siga el comportamiento de una compuerta lógica AND o una compuerta OR.

\[y = AND(x_1,x_2)\]

$x_1$	$x_2$	$y$
$0$	$0$	$0$
$0$	$1$	$0$
$1$	$0$	$0$
$1$	$1$	$1$

Para simular dicho comportamiento, se necesitan 3 pesos sinápticos, 2 para las entradas y el valor del umbral.

\[a = \omega_0 + \omega_1 x_1 + \omega_2 x_2\]

Haciendo $\omega_0 = -1.5$, $\omega_1 = \omega_2 = 1$, se cumple la tabla de verdad para la compuerta AND.

\[a_{AND} = -1.5 + x_1 + x_2\]

Por otro lado, haciendo $\omega_0 = -0.5$ la neurona seguiría el comportamiento de la compuerta OR.

\[y = OR(x_1,x_2)\] \[a_{OR} = -0.5 + x_1 + x_2\]

$x_1$	$x_2$	$y$
$0$	$0$	$0$
$0$	$1$	$1$
$1$	$0$	$1$
$1$	$1$	$1$