Unidades l贸gicas de umbral
Neurona de McCulloh - Pitts
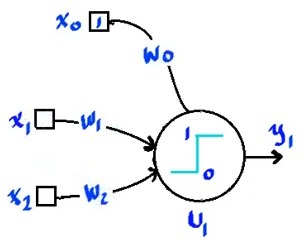
Es una neurona cuyas entradas pueden adquirir los valores $\left{0,1\right}$, al igual que la salida. Utiliza la funci贸n de activaci贸n escal贸n unitario.
Esta es una de las primeras unidades l贸gicas de umbral, que demostr贸 que se pueden obtener diferentes respuestas, siguiendo por ejemplo el comportamiento de una compuerta l贸gica AND u OR.
El comportamiento de esta neurona se pude visualizar utilizando el espacio de entradas:
\[a = \omega_0 + \omega_1 x_1 + \omega_2 x_2\]Nos interesa conocer el comportamiento donde $a$ cambia, en este caso la funci贸n escal贸n unitario cambia en $a = 0$.
\[0 = \omega_0 + \omega_1 x_1 + \omega_2 x_2\] \[\tag{1} x_2 = -\frac{\omega_1}{\omega_2}x_1-\frac{\omega_0}{\omega_2}\]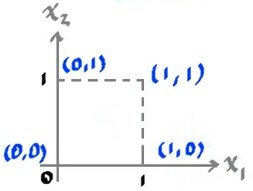
Como se puede apreciar en $(1)$, la ecuaci贸n es una recta dicha recta describe el comportamiento de la neurona, donde todos los valores encima de la recta ser谩n valores de activaci贸n y los que esten por debajo ser谩n valores donde la neurona no ser谩 activada.
Por ejemplo para una compuerta OR, una posible recta ser铆a la siguiente:
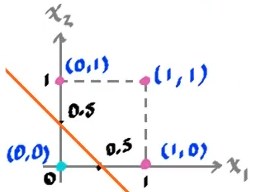
Para una AND se puede proponer est谩 otra:
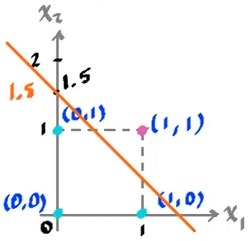
En general la l铆nea trazada representa la Frontera de desisici贸n. Los valores por encima representan las combinaciones de las entradas que activan la neurona y los valores por debajo los que no logran activarla.
La analog铆a que entre las dem谩s partes de la neurona artificial es la siguiente:
\[\underbrace{\omega_i}_\text{Codificaci贸n del conocimiento}:\underbrace{\Sigma}_\text{Integraci贸n de la informaci贸n}:\underbrace{f}_\text{Desici贸n}\]