• Notas
• 7mo Semestre
• Sistemas Neurodifusos

Funciones de membresía básicas

Formulación y parametrización

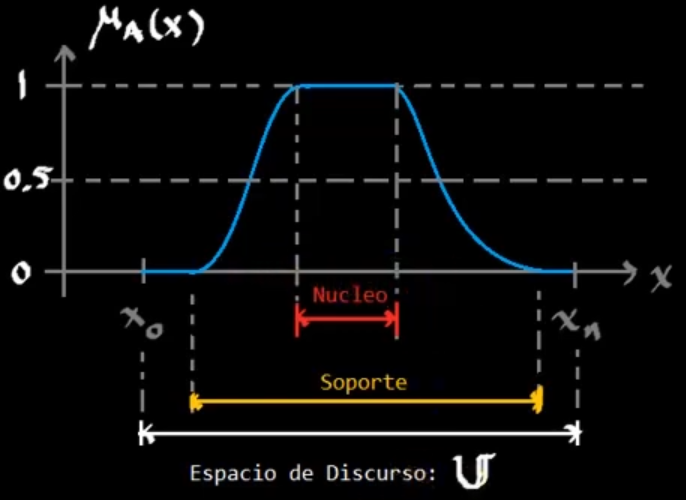
Soporte

Es un conjunto en el dominio y un subconjunto del espacio de discurso donde los valores de A son mayores a 0.

\[\text{Soporte de }A = \left\{x\in\mathbb{U}|: \mu_A(x) > 0\right\}\]

Núcleo o Kernel

Es un conjunto en el dominio, un subconjunto del espacio de discurso y un subconjunto del soporte, donde los valores de A son 1.

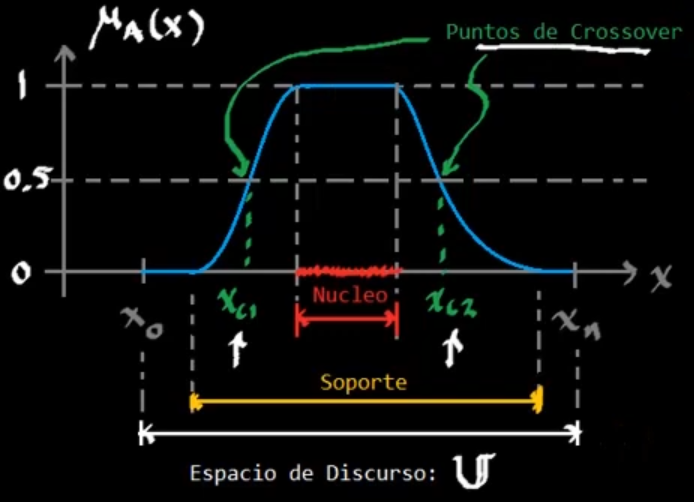
\[\text{Núcleo de }A = \left\{x\in\mathbb{U}|: \mu_A(x) = 1\right\}\]

Puntos de crossover

Son los puntos en la función de membresía donde $\mu(x) = 0.5$

\[\text{Puntos de crossover} = \left\{x_{C1},x_{C2}\in\mathbb{U}|: \mu_A(x_{C1}) = \mu_A(x_{C2}) = 0.5\right\}\]

Corte $\alpha$

\[A_\alpha = \left\{x\in\mathbb{U}|: \mu_A(x) \geq \alpha \right\}\]

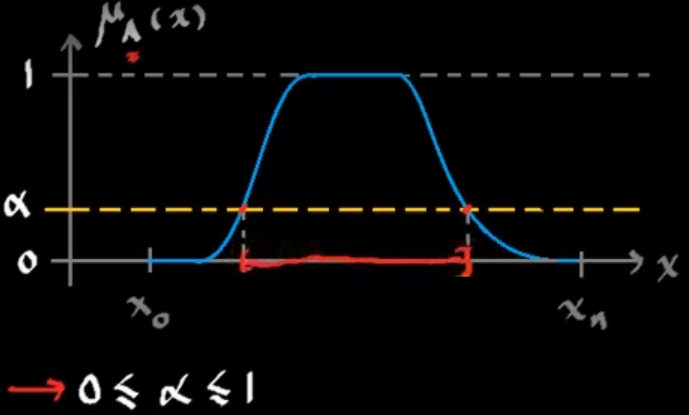
Corte $\alpha$ fuerte

\[A_\alpha = \left\{x\in\mathbb{U}|: \mu_A(x) > \alpha \right\}\]

Funciones de membresía unidimensionales

Dominios continuos

Trapezoidal

\[\mu_A(x) = \begin{cases} 0&x<a\\ \\ \dfrac{x-a}{b-a}&a\leq x<b\\ \\ 1&b\leq x\leq c\\ \\ \dfrac{d-x}{d-c}&c< x\leq d\\ \\ 0&x>d\\ \end{cases}\] \[\mu_A(x) = \text{MF\_TRAP}(x;a,b,c,d)\]

Gaussiana

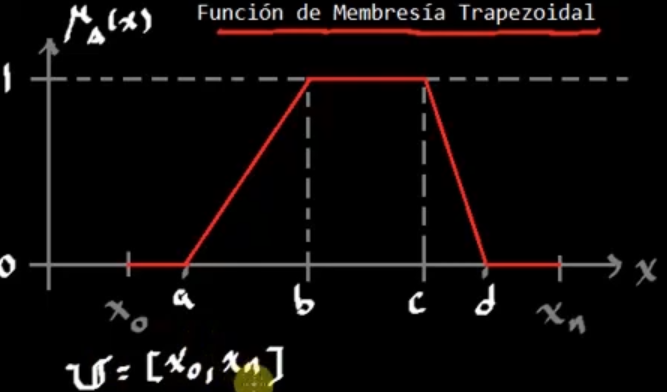
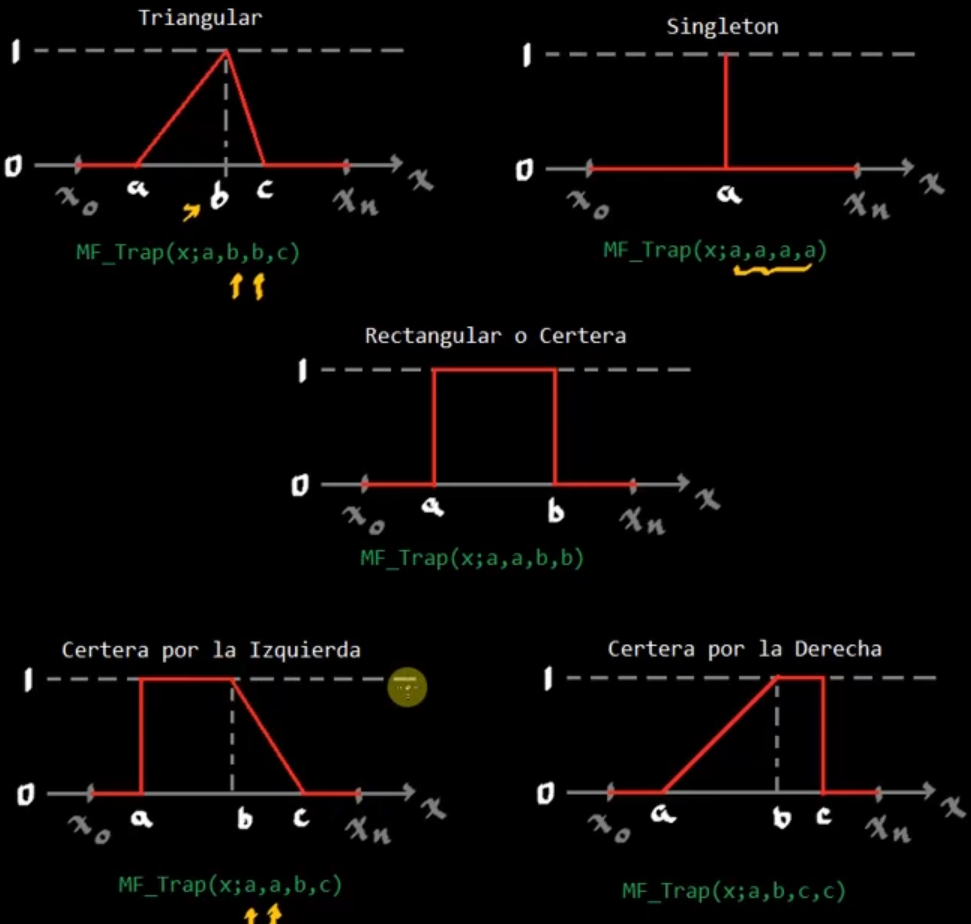
\[\mu_A(x) = e^{\frac{1}{2}(\frac{x-c}{\sigma})^2}\] \[\mu_A(x) = \text{MF\_Gauss}(x;c,\sigma)\]

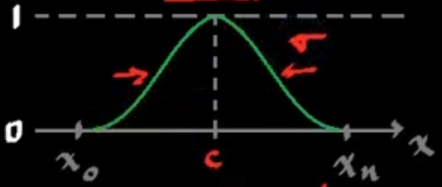
Campana generalizada

\[\mu_A(x) = \dfrac{1}{1+\left|\dfrac{x-c}{a}\right|^{2b}}\] \[\mu_A(x) = \text{MF\_Bell}(x;a,b,c)\]

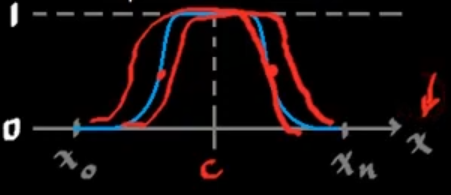
Dominios discretos

\[x\in\mathbb{Z}\quad;\quad\mu_A: \mathbb{Z} \mapsto[0,1]\] \[\mathbb{U} = {0,1,2,3,4,5,6}\] \[\begin{aligned} A &= \{x,\mu_A(x)|: x\in\mathbb{U}\}\\ &=\{(0,0),(1,0.3),(2,0.6),(3,1),(4,0.55),(5,0.2),(6,0.1)\}\\ &=0/0+1/0.3+2/0.6+3/1+4/0.55+5/0.2+6/0.1 \end{aligned}\]

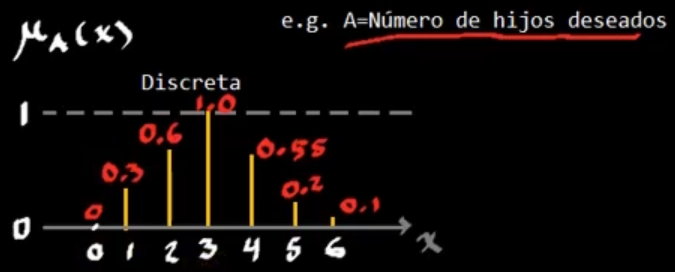
$+$ denota unión, y $/$ denota membresía.

Conjuntos difusos discretos no ordenables

Algunos conjuntos no se pueden ordenar:

\[\mathbb{U} = {0,1,2,3,4,5,6}\] \[\begin{aligned} B&=\{(CDMX,0.7),(Celaya,0.1),(Cancún,0.1)\}\\ B&=CDMX/0.7+Celaya/0.1+Cancún/0.1\\ \end{aligned}\]