Introducci贸n a la l贸gica difusa
Conjuntos cl谩sicos
\[A = \{x \in \mathbb{R} | x\geq 6\} = [6, \infty)\]Se puede observar que:
\[5 \in A\quad 7\cancel\in A\]En los conjuntos cl谩sicos se tienen l铆mites bien definidos. En este caso dado por el n煤mero 6.
Otra notaci贸n para expresar que 5 no pertenece a A, es la siguiente:
\[5\cancel\in A\quad\longleftrightarrow\quad(5,0)\] \[5\cancel\in A\quad\longleftrightarrow\quad(7,0)\]Ecuaci贸n caracter铆stica de un conjunto
L贸gica difusa
Supongamos que se tienen los siguientes conjuntos A, de vasos vac铆os, es decir al 0% y B de vasos llenos (100%).
Para conjuntos cl谩sicos, tendr铆amos lo siguiente:
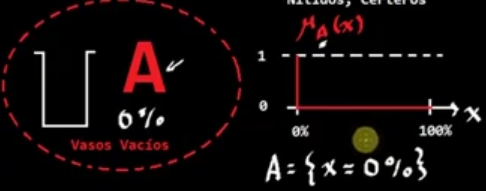
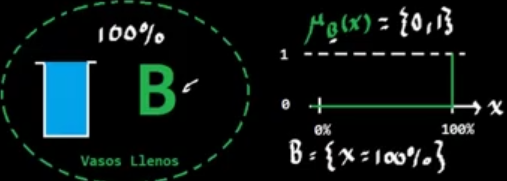
Pero esto es demasiado estricto y s贸lo dejan 1 valor en cada conjunto.
Para esto Lofti Zadeh crea la l贸gica difusa.
Conjuntos difusos
Para los conjuntos anteriores se puede definir la siguiente funci贸n de membres铆a o relaci贸n difusa.
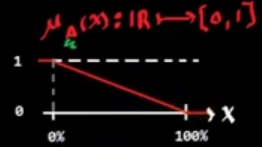
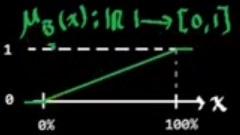
Ahora bien, suponiendo que se tienen los siguientes vasos:
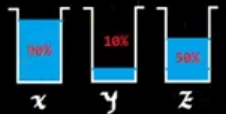
En este caso podemos observar:
\[\begin{aligned} \mu_A(x)&=0.1\\ \mu_A(x)&=0.9\\ \mu_A(z)&=0.5\\ \end{aligned}\qquad \begin{aligned} \mu_B(x)&=0.9\\ \mu_B(x)&=0.1\\ \mu_B(z)&=0.5\\ \end{aligned}\]Esto es una forma mucho m谩s acercada a como pensamos los humanos pues el concepto de estar lleno, es relativo y puede ser que 0.9 este lleno dependiendo del contexto.
As铆 mismo las funciones de membres铆a pueden ser diferentes, por ejemplo una funci贸n sigmoide:
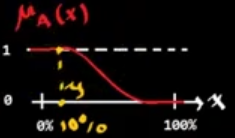
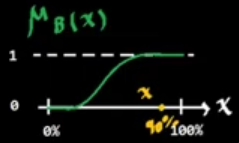
El cambio en estas funciones es dado por la subjetividad.
Definici贸n
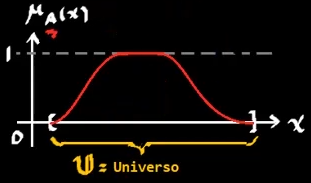
Un conjunto difuso se define de la siguiente forma:
\[A = \{(x,\mu(x))|: x \in \mathbb{U}\}\]Donde:
$\mu(x)$ = Funci贸n de membres铆a
$\mathbb{U}$ = Conjunto universo o espacio de discurso
Variable linguist铆ca
Es una palabra que puede ser sustituida por otra palabra dentro de un conjunto difuso.
Ejemplo
\[\text{Estatura} = \{\text{Baja},\text{Media},\text{Alta}\}\]La estatura puede ser baja, media o alta.