• Notas
• 7mo Semestre
• Sistemas Neurodifusos

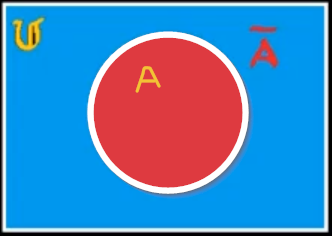
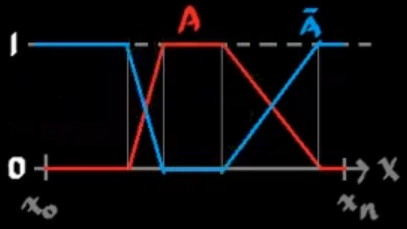
Operaciones lógicas con conjuntos difusos

En conjuntos difusos, para que un elemento pertenezca a un conjunto difuso, basta con que su membresía sea mayor que 0.

\[\begin{aligned} A=\left\{x,\mu_A(x)|:\mu_A(x)>0\right\}\\ B=\left\{x,\mu_B(x)|:\mu_B(x)>0\right\}\\ \end{aligned}\]

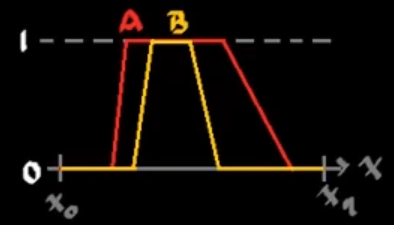
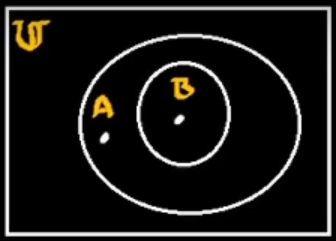
En este caso:

\[B\subset A\] \[\begin{aligned} &\forall x |:\mu_B(x)>0 \rightarrow \mu_A(x) > 0\\ &\exists x, mu_A(x)>0 |:\mu_B(x)=0\\ \end{aligned}\]

En este caso, esto es cierto, pero si se tiene el siguiente ejemplo:

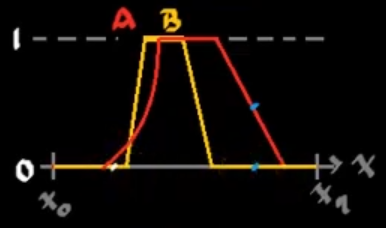
En esto caso el enunciado anterior, es falso. Puesto que existen elementos en B que tienen mayor membresía en B que en A.

Subconjunto

Por lo que en general la expresión de subconjunto es la siguiente:

\[B\subset A\] \[\forall x \in \mathbb{U} |: \mu_B(x)>0 \rightarrow\mu_A(x)\geq\mu_B(x)\]

Unión difusa

\[A \cup B = \left\{x\in\mathbb{U}:x\in A\quad\text{ó}\quad x\in B\right\}\] \[\begin{cases} \mu_{A\cup B}(x) \geq \mu_A(x)\\ \mu_{A\cup B}(x) \geq \mu_B(x)\\ \end{cases}\quad;\quad \forall x \in \mathbb{U}\]

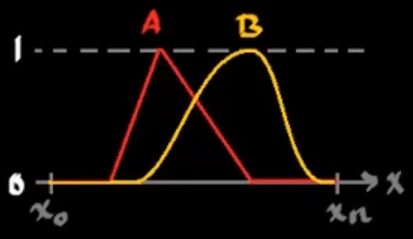
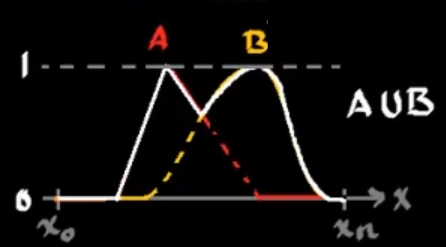
Por lo tanto:

\[\mu_{A\cup B} = \text{MAX}[\mu_A(x),\mu_B(x)]\] \[A\cup B = \left\{x,\mu_{A\cup B}(x)|:\mu_{A\cup B} = \text{MAX}[\mu_A(x),\mu_B(x)]\right\}\]

Intersección difusa

\[A \cap B = \left\{x\in\mathbb{U}:x\in A\quad\text{y}\quad x\in B\right\}\]

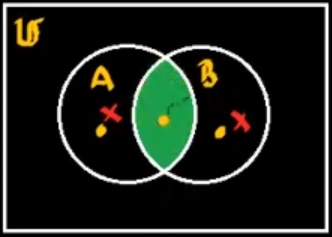
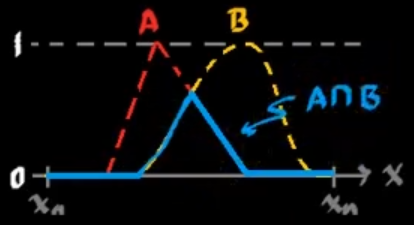
Por lo tanto:

\[\mu_{A\cap B} = \text{MIN}[\mu_A(x),\mu_B(x)]\] \[A\cap B = \left\{x,\mu_{A\cup B}(x)|:\mu_{A\cup B} = \text{MIN}[\mu_A(x),\mu_B(x)]\right\}\]

Complemento difuso

\[\begin{aligned} \bar{A} &= \left\{x\in\mathbb{U}|: x\notin A\right\}\\ &= \left\{x,\mu_{\bar{A}}(x)|: \mu_{\bar{A}}(x) = 1 - \mu_A(x)\right\}\\ \end{aligned}\]

Convención de notación

\[\begin{cases} A\cup B = \text{OR}(A,B) = \text{MAX}(A,B) &\rightarrow \text{MAX}(\mu_A(x),\mu_B(x))\\ \\ A\cap B = \text{AND}(A,B) = \text{MIN}(A,B) &\rightarrow \text{MIN}(\mu_A(x),\mu_B(x))\\ \\ \bar{A} = \text{NOT}(A) = 1-A &\rightarrow 1-\mu_A(x) \end{cases}\]