Razonamiento difuso
La regla IF - THEN
En lógica los razonamientos, de inferencia son de este tipo:
Premisa 1 (Hecho): $x$ es $A$
Premisa 2 (Regla): si $x$ es $A$, entonces $y$ es $B$
$\overline{\hphantom{Premisa 1 (Regla): si x es A, entonces y es B}}$
Conclusión (Consecuencia): $y$ es $B$
Pero esto aplica para conjuntos certeros, en caso de conjuntos difusos se utiliza el denominado razonamiento aproximado.
Razonamiento aproximado
En este caso, se tienen conjuntos difusos, por lo tanto, el razonamiento aproximado utiliza conjuntos difusos.
Premisa 1 (Hecho): $x$ es $A’$
Premisa 2 (Regla): si $x$ es $A$, entonces $y$ es $B$
$\overline{\hphantom{Premisa 1 (Regla): si x es A, entonces y es B}}$
Conclusión (Consecuencia): $y$ es $B’$
Inferencia tipo Mamdani
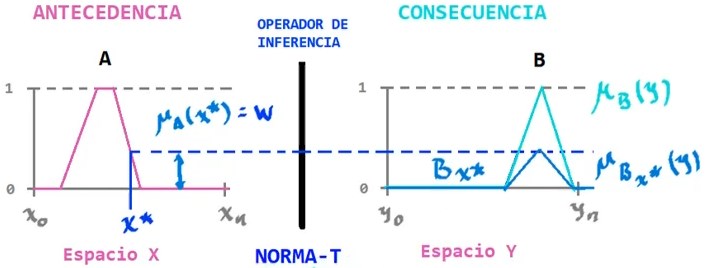
Ebrahim Mamdani, propuso este modelo de inferencia para razonamiento aproximado, donde podemos ver que primero se obtiene $w$ a partir de la antecedencia, que es la intensidad de disparo de la regla, luego por medio de un operador de inferencia; una Norma-T, se obtiene el conjunto correspondiente de consecuencia.
\[B_x* = T(w,\mu_B(y))\]Al ser el operador de inferencia una Norma-T, se puede utilizar el mínimo (MIN) o el producto (PROD) por ejemplo.
Multiples antecedencias
Para el caso de razonamientos con interseccion:
Premisa 1 (Hecho): $x$ es $A’$
Premisa 2 (Hecho): $y$ es $B’$
Premisa 3 (Regla): si $x$ es $A$ y $y$ es $B$, entonces $z$ es $C$
$\overline{\hphantom{Premisa 1 (Regla): si x es A, entonces y es natonces}}$
Conclusión (Consecuencia): $z$ es $C’$
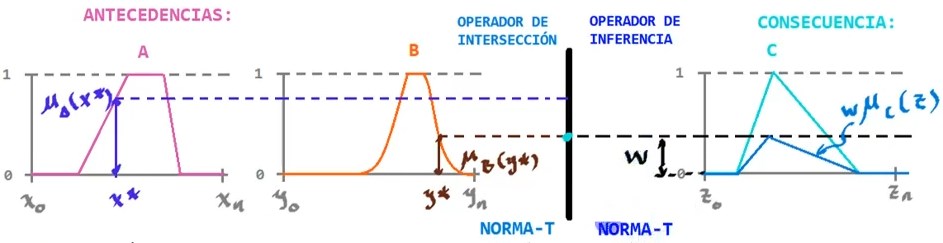
En este caso, se utiliza un operador de intersección antes, que también es una Norma-T y es independiente de la utilizada en el operador de inferencia.
\[w = \text{NORMA-T}_{inter}(\underbrace{\mu_A(x*)}_{A'},\underbrace{\mu_B(y*)}_{B'})\] \[w = \text{NORMA-T}_{infer}(w,\mu_C(z))\]Multiples reglas
Para el caso de cuando existe más de una regla, por ejemplo
$R_1$: si $x$ es $A_1$ y $y$ es $B_1$, entonces $z$ es $C_1$
$R_2$: si $x$ es $A_2$ y $y$ es $B_2$, entonces $z$ es $C_2$
Dependiendo del razonamiento, se puede utilizar la agregación o sustracción de las reglas, es decir, utilizando la Norma-S o Norma-T respectivamente:
\[\begin{aligned} R_1 \text{or} R_2 &= \text{NORMA-S}(C_1',C_2')\\ \\ R_1 \text{and} R_2 &= \text{NORMA-T}(C_1',C_2')\\ \end{aligned}\]