Control de velocidad en lazo cerrado para un motor de CD
Como se vio en el curso de control, el controlador pid tiene la siguiente forma:
\[\tag{1} C(s) = K_p + \frac{K_i}{s} + K_d s\]Sin embargo, esta funci贸n de transferencia no es propia y su implementaci贸n en f铆sico se complica, adem谩s el t茅rmino derivador amplifica altas frecuencias, pues es un filtro pasa altas con polo en el infinito. Por ende esto puede incrementar el ruido, para ello se implementa con un filtro pasa-bajas. Quedando la funci贸n de transferencia de la siguiente forma:
\[\tag{2} C(s) = K_p + \frac{K_i}{s} + K_d \frac{Ns}{s + N}\]Donde $N$ es la frecuencia de corte del filtro pasa-bajas.
A $(2)$ se le conoce como controlador PID de banda limitada. Simplificando la expresi贸n:
\[\tag{3} C(s) = \frac{(K_p + K_d N)s^2 + (K_i + K_p N)s + K_iN}{s^2 + Ns}\]As铆, se reduce el ruido y la funci贸n de transferencia ya es propia, haciendo m谩s f谩cil su implementaci贸n.
Implementaci贸n en Simulink
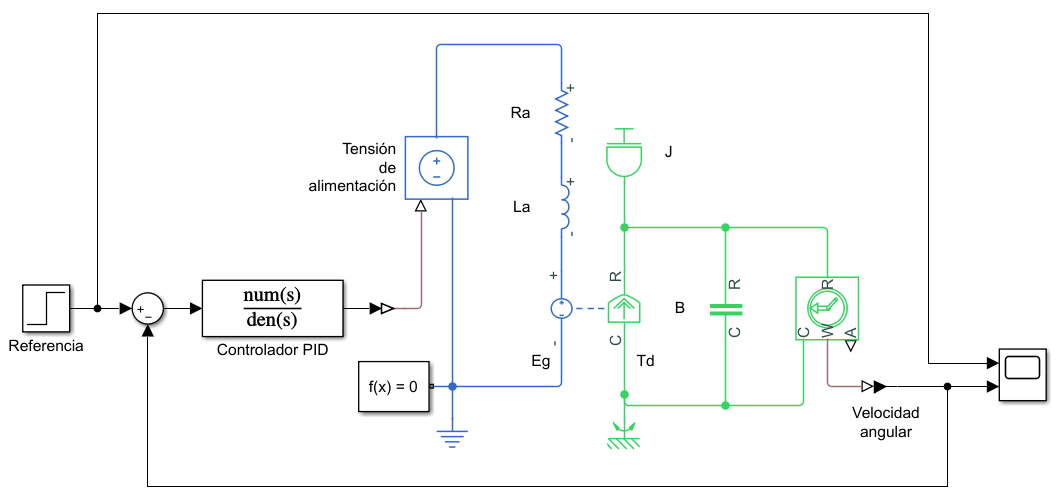
Como par谩metros se utilizaron los mismos que en el control de velocidad en lazo abierto:
\[\begin{aligned} J &= 0.01\text{ kg.m}^2\\ B &= 0.1\text{ N.m}\\ K_v &= 0.01 \frac{\text{V}}{\frac{\text{rad}}{\text{s}}}\\ K_t &= 0.01 \frac{\text{N.m}}{\text{A}}\\ R_a &= 1 \Omega\\ L_a &= 0.5 \text{ H}\\ \end{aligned}\]En el controlador, se utilizaron los siguientes coeficientes:
\[\begin{aligned} K_p &= 100\\ K_i &= 200\\ K_d &= 10\\ N &= 100\\ \end{aligned}\]Quedando la funci贸n de transferencia como:
\[C(s) = \frac{1100s^2 + 10200s + 20000}{s^2+100s}\]Resultado
Se recabaron los datos de control de lazo abierto, cerrado y sin control para realizar la siguiente comparativa:
Se puede observar, que el control en lazo cerrado es m谩s r谩pido que el de lazo abierto y ambos llegan a la referencia en el estado estacionario.
Por lo que los controladores en lazo cerrado permiten alcanzar un mejor desempe帽o, sin embargo acarrean consigo un costo mayor de implementaci贸n.