Control discreto de velocidad en lazo cerrado para un motor de CD
Modelo en Simulink
La diferencia de este modelo y el utilizado para tiempo continuo, es que el controlador se implementa dentro de dos retenedores de orden cero que simulan el paso entre continuo y discreto como lo ser铆a en la pr谩ctica por medio de convertidores anal贸gicos digitales o viceversa.
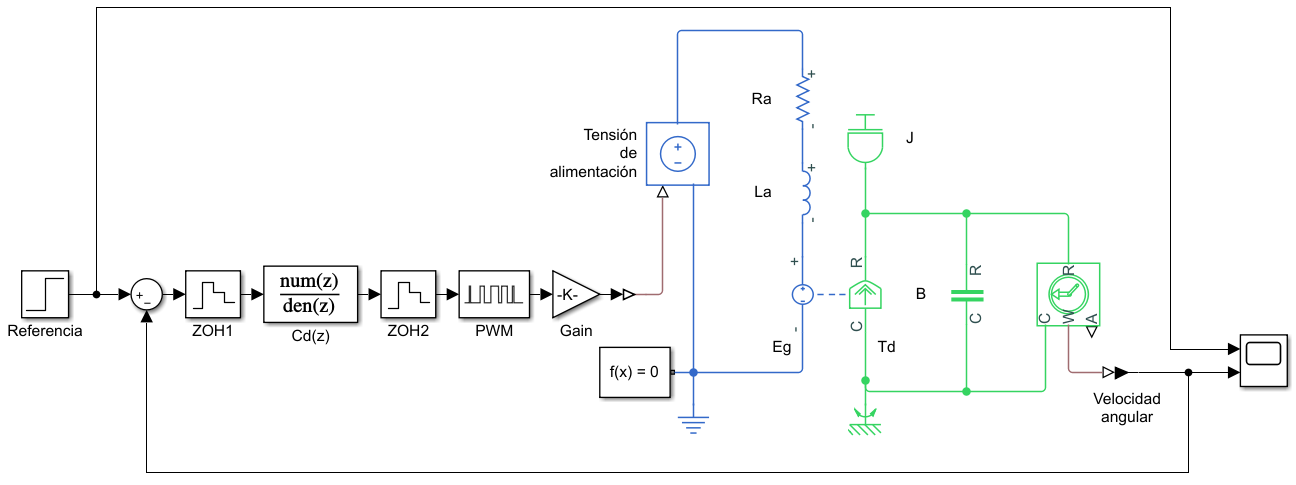
Como se puede observar, la ganancia se aplic贸 despu茅s del controlador puesto que se busca reducir la probabilidad de desbordamiento aritm茅tico, que puede ocurrir al tener n煤mero muy grandes o muy peque帽os. As铆, se busca que la ganancia del controlador sea de aproximadamente 1 y la ganancia se aplica despu茅s. Para esto es necesario dividir sobre la ganancia en la ecuaci贸n del controlador PID:
\[u(t)=e(t)+\frac{K_i}{K_p}\int e(t)dt + \frac{K_d}{K_p}\dfrac{de(t)}{dt}\]Adem谩s, se utiliz贸 un PWM a la salida puesto que normalmente se regula as铆 la tensi贸n en aplicaciones reales.
Implementaci贸n de sistema de control
El motor tiene los siguientes par谩metros:
\[\begin{aligned} J &= 0.01\text{ kg.m}^2\\ B &= 0.1\text{ N.m}\\ K_v &= 0.01 \frac{\text{V}}{\frac{\text{rad}}{\text{s}}}\\ K_t &= 0.01 \frac{\text{N.m}}{\text{A}}\\ R_a &= 1 \Omega\\ L_a &= 0.5 \text{ H}\\ \end{aligned}\]Para discretizar el sistema de control, se comenzar谩 por obtener el controlador en tiempo continuo:
s = tf('s')
M = K / ((J*s+b)*(L*s+R)+K^2);
M = minreal(M)
Utilizando el controlador PID de banda limitada, pero con ganancia unitaria:
\[\tag{2} C(s) = 1 + \frac{K_i}{K_p}\frac{1}{s} + \frac{K_d}{K_p}\frac{Ns}{s+N}\]Se utilizaran los siguientes valores de coeficientes:
\[\begin{aligned} K_p &= 100\\ K_i &= 200\\ K_d &= 10\\ N &= 100\\ \end{aligned}\]C = tf(pid(1,Ki/Kp,Kd/Kp,N))
C = minreal(C)
Discretizaci贸n
Primero se busca conocer la frecuencia de muestreo del sistema del sistema:
% Funci贸n de transferencia en lazo cerrado
G = minreal(feedback(C*Kp*M,1));
% Ancho de banda
Bw = bandwidth(G)/(2*pi);
% frecuencia de muestreo
fs = 10*Bw
La frecuencia de muestreo, seg煤n el teorema de muestreo de Nyquist-Shanon debe ser mayor que el doble del ancho de banda del sistema.
Ahora se obtiene la aproximaci贸n del sistema continuo a digital:
h = 1/fs;
Cd = c2d(C,h,'Tustin')
$h$ es el valor que se debe utilizar como tiempo de muestreo en los bloques PWM y el primer retenedor de orden 0, en realidad el segundo retenedor no es necesario pero est谩 como representaci贸n de un convertidor DAC.
Resultado
