• Notas
• 8vo Semestre
• Procesador Digital de Señales

Filtros digitales

Filtros

Los filtros son fundamentales en el procesamiento digital de señales y son los filtros digitales los más ampliamente usados en este campo. Los filtros sirven para operar en distintas frecuencias sobre distintos fines. Los tipos de filtros más comunes son los siguientes:

• Filtros pasa bajas: Atenúan frecuencias altas.
• Filtros pasa altas: Atenúan frecuencias bajas.
• Filtros pasa bandas: Atenúan frecuencias fuera de un rango.
• Filtros rechaza bandas: Atenúan frecuencias dentro de un rango.
• Filtros de peine: Atenúan una cierta frecuencia y todos sus armónicos.
• Filtros pasa todo: No atenúan ninguna frecuencia pero puede modificar la fase.

Todos estos tipos de filtros pueden ser implementados de forma analógica o digital. Los filtros analógicos han sido muy estudiados y se consiguen resultados muy buenos en su implementación, sin embargo, al ser sistemas analógicos, como desventaja que su comportamiento varía con la temperatura y el tiempo. En procesamiento digital de señales por lo general se ocupan filtros digitales porque tienen las siguientes ventajas:

• Son programables, no es necesario cambiar el circuito, sólo el programa
• Dos filtros idénticos se compartan idéntico
• Su comportamiento no varía con el tiempo y la temperatura

En los filtros digitales existen 2 tipos, los filtros de respuesta finita al impulso FIR y los filtros de respuesta infinita al impulso IIR.

Funcionamiento de un filtro digital

Se parte de la respuesta discreta al impulso, por medio de la suma de convolución:

\[y[n] = \sum^\infty_{k=0} b[k]x[n-k]\]

Donde:
$y$ es la salida
$x$ es la entrada
$b$ es la respuesta al impulso

Transformando esta forma, en una parte finita y otra infinita $O(u,n)$:

\[y[n] = \sum^N_{k=0} b[k]x[n-k] + O(u,n)\]

Filtro de respuesta infinita al impulso IIR

$O(u,n)$ debe ser una función computable, ya que en realidad no es posible con sistemas digitales obtener una respuesta que tiende a infinito. Por ejemplo, la siguiente función no es computable:

\[O(x,n) = \sum^\infty_{k=N+1} b[k]x[n-k]\]

Así que se busca otra función, como:

\[O(y,n) = - \sum^M_{k=1}a[k]y[n-k]\]

Entonces se tiene retroalimentación de la salida, lo que permite tener un acercamiento al comportamiento en infinito y es computable. La forma del filtro IIR es la siguiente:

\[\boxed{y[n] = \sum^N_{k=0} b[k]x[n-k] - \sum^M_{k=1}a[k]y[n-k]}\]

Sin embargo, ya que el sistema tiene retroalimentación, esto conlleva a problemas de estabilidad y entonces los coeficientes $a[n]$ se vuelven importantes, puesto que de no calcularlos bien, el filtro no sirve.

Su función de transferencia es la siguiente:

\[G(z) = \frac{b_0 + b_1z^{-1} + b_2z^{-2} + \cdots + b_Nz^{-N}}{1 + a_1z^{-1} + a_2z^{-2} + \cdots + a_Mz^{-M}}\]

Su implementación en Simulink para un filtro IIR de orden 2 es la siguiente:

Y su salida es la siguiente:

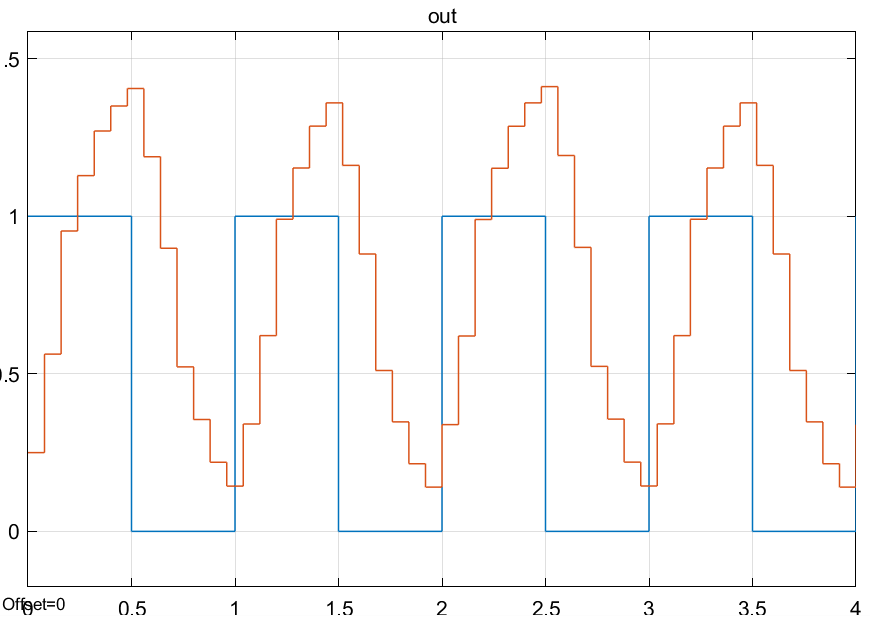
Filtro de respuesta finita al impulso FIR

El filtro FIR es un filtro no recursivo, o sea que se utilizan las entradas previas en el filtro sólamente. Es decir, se suponen los coeficientes $a[n] = 0$ y tiene la siguiente forma:

\[\boxed{y[n] = \sum^N_{k=0} b[k]x[n-k]}\]

Su implementación en Simulink es la siguiente:

Como se puede ver, tiene un retardo de la señal, en este caso, 3 retardos, que luego se suman, ponderando una ganancia de 1. La salida es la siguiente:

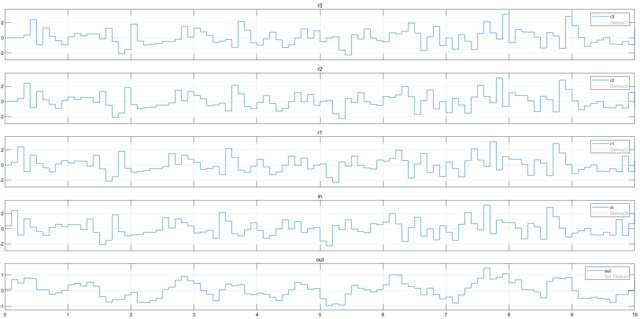
Como se puede ver, en la señal de salida (out) es más fácil ver la tendencia de la señal.

En este caso el filtro FIR implementado es de orden 3, pues hay 3 retardos. Pero pueden ser de orden $n$ y la expresión de su función de transferencia es la siguiente:

\[T(z) = a_0 + a_1z^{-1} + a_2z^{-1} + \ldots + a_nz^{-1}\]