• Notas
• 8vo Semestre
• Tópicos Avanzados de Sensores

Microacelerómetro

Tomando en cuenta el sistema mása resorte amortiguador:

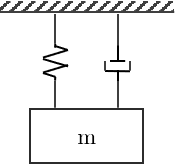
Para medir el desplazamiento de $m$ se utiliza un circuito de capacitores diferenciales

Su circuito equivalente es el siguiente:

\[V_o = V_s - V_{C1}\] \[\begin{aligned} q_1 &= C_1(V_s - V_o)\\ q_2 &= C_2(V_o + V_s)\\ \end{aligned}\] \[\begin{aligned} C_1(V_s - V_o) &= C_2(V_o + V_s)\\ C_1V_s - C_1V_o &= C_2V_o + C_2V_s\\ C_1V_s - C_2V_s &= C_1V_o + C_2V_o\\ \end{aligned}\] \[\boxed{V_o = \frac{C_1 - C_2}{C_1 + C_2} V_s}\]

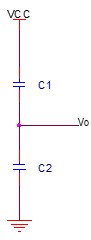
Como

\[C_1 = \frac{1}{G_1}\qquad C_2 = \frac{1}{G_2}\]

Entonces

\[\boxed{V_o = \frac{G_2 - G_1}{C_1 + C_2} V_s}\]

Funcionamiento general

• La aceleración produce un desplazamiento en el sensor.
• El desplazamiento genera un cambio en los valores de las capacitancias.
• El cambio en las capacitancias produce una tensión de salida.

Modelo matemático

\[\tag{1} m\ddot{x} + b\dot{x} + kx = F = ma\]

Aplicando la transformada de Laplace en $(1)$ con $c.i. = 0$.

\[\tag{2} \begin{aligned} \frac{X(s)}{\large a(s)} &= \frac{m}{m s^2 + bs + k}\\ &= \frac{1}{s^2 + \frac{b}{m}s + \frac{k}{m}}\\ \end{aligned}\]

Comparando el sistema con la función de transferencia general para sistemas de segundo orden:

\[\dfrac{C(s)}{R(s)}=\dfrac{\omega_n^2}{s^2+2\xi\omega_n s +\omega_n^2}\]

Podremos estimar cual es la frecuencia natural del sistema y su factor de amortiguamiento.

\[\omega_0 = \sqrt{\frac{k}{m}}\] \[\xi = \frac{b}{2\sqrt{km}}\]

Siendo $a$ constante en $(2)$, se puede determinar el valor de $x$ en estado estacionario.

\[\boxed{x = \frac{ma}{k}}\]

Método del trapecio

\[a(t)= a(t_1) + \frac{a(t_2) - a(t_1)}{t_2 - t_1}(t - t_1)\] \[\begin{aligned} v(t) &= \int^{t_2}_{t_1}a(t)dt = a(t_1)\int^{t_2}_{t_1}dt + \frac{a(t_2) - a(t_1)}{t_2 - t_1}\int^{t_2}_{t_1}(t - t_1)dt\\ &= a(t_1)[t_2 - t_1] + \frac{a(t_2) - a(t_1)}{t_2 - t_1}\frac{(t_2 - t_1)^2}{2} \end{aligned}\]

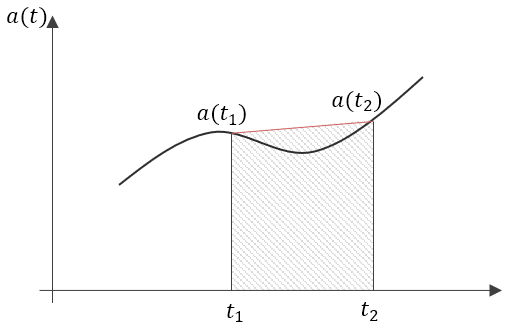
Por lo tanto

\[\boxed{v(t) = (t_2 - t_1)\frac{a(t_1) + a(t_2)}{2}}\]