image/svg+xml

Cinemática directa

Matrices de rotación

Son matrices que describen una operación de rotación:

p0=R10p1p^{0} = R^{0}_1 p^{1}

Donde:
p0p^0 es el punto en el marco 00.
R10R^0_1 es la matriz de rotación que vincula el marco 11 hacia el marco 00.
p0p^0 es el punto en el marco 11.

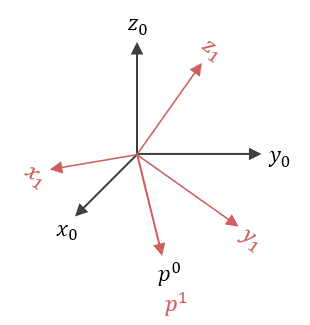
Dos ejes coordenados con el mismo punto

Los puntos son físicamente el mismo, pero sus descripciones cambian dependiendo del marco. Las matrices de rotación sirven como traductoras entre marcos coordenados.

Construcción de una matriz de rotación

La construcción de una matriz de rotación, se puede hacer mediante la técnica de proyección:

R10=[x1⋅x0y1⋅x0z1⋅x0x1⋅y0y1⋅y0z1⋅y0x1⋅z0y1⋅z0z1⋅z0]R^0_1 = \begin{bmatrix} x_1 \cdot x_0 & y_1 \cdot x_0 & z_1 \cdot x_0\\ x_1 \cdot y_0 & y_1 \cdot y_0 & z_1 \cdot y_0\\ x_1 \cdot z_0 & y_1 \cdot z_0 & z_1 \cdot z_0\\ \end{bmatrix}